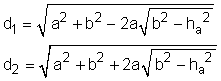| The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry. |

|

Home  Analytic Geometry Analytic Geometry  Quadrilateral Quadrilateral  Parallelogram and Rhombus Parallelogram and Rhombus |
|||||||||||||||||||
| See also: Quadrilateral - General Definitions, Rectangle and Square, Tangential Quadrilateral | |||||||||||||||||||






|
|||||||||||||||||||
Parallelogram and Rhombus
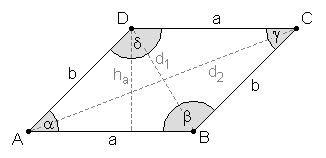 A parallelogram is a quadrilateral with parallel opposite sides. As a consequence of the parallel sides the opposite angles are equal:
A parallelogram is a quadrilateral with parallel opposite sides. As a consequence of the parallel sides the opposite angles are equal:
α = γ, and β = δ.
A parallelogram with equal sides (a = b) is called a rhombus, a parallelogram whose angles are all right angles is called a rectangle.
The diagonals of a parallelogram bisect each other, the diagonals of a rhombus intersect at a right angle. The diagonals and the sides of a parallelogram are related by the following equation: d12 + d22 = 2(a2 + b2) If the sides a and b of a parallelogram are given as vectors u = AB and v = AD, then the area of the parallelogram can be calculated by the cross product of the two vectors: A = uxv
|
|||||||||||||||||||
Home  Analytic Geometry Analytic Geometry  Quadrilateral Quadrilateral  Parallelogram and Rhombus Parallelogram and Rhombus |
|||||||||||||||||||
Last Update: 2011-01-11


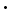 ha = ab
ha = ab