| The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry. |

|

Home  Analytic Geometry Analytic Geometry  Triangle Triangle  Relations between Angles and Sides Relations between Angles and Sides |
|
| See also: Congruence Transformation, Congruent and Similar Triangles, Relations between Angles in Triangles, Half Angle Relations in a Triangle, Mollweide's Formulas, Construction of a Triangle | |






|
|
Relations between Angles and Sides in TrianglesThe following list summarizes the most important relationships between the angles and the sides in an arbitrary triangle: 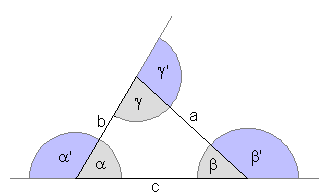
|
|
Home  Analytic Geometry Analytic Geometry  Triangle Triangle  Relations between Angles and Sides Relations between Angles and Sides |
|
Last Update: 2011-01-11

