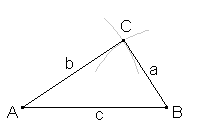
Construction of a Triangle
The construction of a triangle is controlled by the congruential theorems. In order to be able to construct a triangle one needs to know three values (either sides S or angles A): SSS, SSA, SAA. Note that it is not sufficient to know only three angles.
| Known items |
Way of construction |
SSS
three sides |
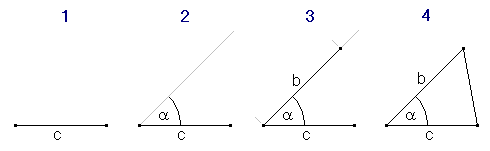
 Given are the line segments AB, BC, and AC. Take one line segment, i.e. AB, draw it horizontally; and use a pair of compasses to draw circles around the endpoints A and B having the radius BC, and AC, respectively. The wanted third point is located at the intersection of the two circles (two solutions which are not congruent). In order to be able to construct a triangle from three segments, one of the segments must be shorter than the sum of the other two: a < b+c, or b < a+c, or c < a+b
Given are the line segments AB, BC, and AC. Take one line segment, i.e. AB, draw it horizontally; and use a pair of compasses to draw circles around the endpoints A and B having the radius BC, and AC, respectively. The wanted third point is located at the intersection of the two circles (two solutions which are not congruent). In order to be able to construct a triangle from three segments, one of the segments must be shorter than the sum of the other two: a < b+c, or b < a+c, or c < a+b |
SSA
two sides, one angle |
In the case of two known sides and one known angle, we have to distinguish two cases: the first case deals with the situation where the known angle is between the two sides; in the second case the known angle is at the end of one side.
 If the known angle is between the two sides we simply have to draw one of the two line segments (c), then add another segment (b) using the common angle α, and finally connect the two end points. If the known angle is between the two sides we simply have to draw one of the two line segments (c), then add another segment (b) using the common angle α, and finally connect the two end points.
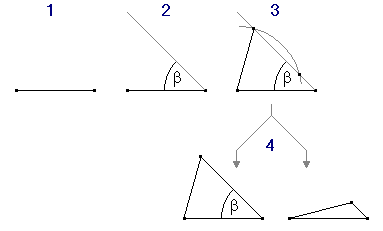 If the known angle is not between the two known sides, one has first to draw the side which is one leg of the angle. Next we draw a line at an angle β to the first side. Then we take a pair of compasses and draw an arc whose radius is the length of the second side. Finally we connect the intersection of the arc to the starting and ending point of the first side. Note that there are usually two solutions. If the second side is two short there could be even no solution at all. If the known angle is not between the two known sides, one has first to draw the side which is one leg of the angle. Next we draw a line at an angle β to the first side. Then we take a pair of compasses and draw an arc whose radius is the length of the second side. Finally we connect the intersection of the arc to the starting and ending point of the first side. Note that there are usually two solutions. If the second side is two short there could be even no solution at all.
|
SAA
one side, two angles |
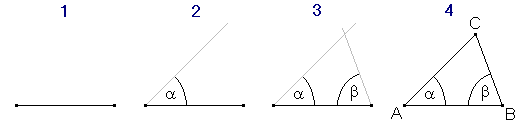 If the two known angles are both adjacent to the known side, we simple draw the side and construct two lines at the known angles α and β. The triangle results from the end points of the known side and the intersection of the two lines. Please note that in the case of two known angles, the third angle is automatically known, too (the sum of all angles in a triangle is 180°, thus the third angle γ is 180-α-β). If the two known angles are both adjacent to the known side, we simple draw the side and construct two lines at the known angles α and β. The triangle results from the end points of the known side and the intersection of the two lines. Please note that in the case of two known angles, the third angle is automatically known, too (the sum of all angles in a triangle is 180°, thus the third angle γ is 180-α-β).
|
|


 Analytic Geometry
Analytic Geometry  Triangle
Triangle  Construction of a Triangle
Construction of a Triangle





 Analytic Geometry
Analytic Geometry  Triangle
Triangle  Construction of a Triangle
Construction of a Triangle

 Given are the line segments AB, BC, and AC. Take one line segment, i.e. AB, draw it horizontally; and use a pair of compasses to draw
Given are the line segments AB, BC, and AC. Take one line segment, i.e. AB, draw it horizontally; and use a pair of compasses to draw  If the known angle is between the two sides we simply have to draw one of the two line segments (c), then add another segment (b) using the common angle α, and finally connect the two end points.
If the known angle is between the two sides we simply have to draw one of the two line segments (c), then add another segment (b) using the common angle α, and finally connect the two end points.
 If the known angle is not between the two known sides, one has first to draw the side which is one leg of the angle. Next we draw a line at an angle β to the first side. Then we take a pair of compasses and draw an arc whose radius is the length of the second side. Finally we connect the intersection of the arc to the starting and ending point of the first side. Note that there are usually two solutions. If the second side is two short there could be even no solution at all.
If the known angle is not between the two known sides, one has first to draw the side which is one leg of the angle. Next we draw a line at an angle β to the first side. Then we take a pair of compasses and draw an arc whose radius is the length of the second side. Finally we connect the intersection of the arc to the starting and ending point of the first side. Note that there are usually two solutions. If the second side is two short there could be even no solution at all.
 If the two known angles are both adjacent to the known side, we simple draw the side and construct two lines at the known angles α and β. The triangle results from the end points of the known side and the intersection of the two lines. Please note that in the case of two known angles, the third angle is automatically known, too (the sum of all angles in a triangle is 180°, thus the third angle γ is 180-α-β).
If the two known angles are both adjacent to the known side, we simple draw the side and construct two lines at the known angles α and β. The triangle results from the end points of the known side and the intersection of the two lines. Please note that in the case of two known angles, the third angle is automatically known, too (the sum of all angles in a triangle is 180°, thus the third angle γ is 180-α-β).