Reactors

Reactors are used in electronic power equipment to smooth out ripple voltage in d-c supplies, so they carry direct current in the coils. It is common practice to build such reactors with air gaps in the core to prevent d-c saturation. The air gap, size of the core, and number of turns depend upon three interrelated factors: inductance desired; direct current in the winding; and a-c volts across the winding.

The number of turns, the direct current, and the air gap determine the d-c flux density, whereas the number of turns, the volts, and the core size determine the a-c flux density. If the sum of these two flux densities exceeds saturation value, noise, low inductance, and non-linearity result. Therefore a reactor must be designed with knowledge of all three of the conditions above.

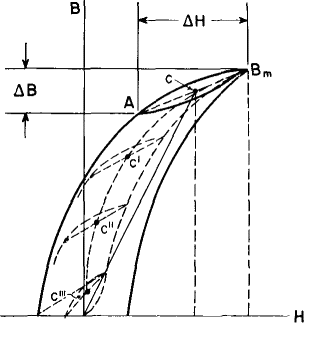
Magnetic flux through the coil has two component lengths of path: the air gap l_g, and the length of the core l_c. The core length l_c is much greater geometrically than the air gap l_g, as indicated in Fig. 57, but the two components do not add directly because their permeabilities are different. In the air gap, the permeability is unity, whereas in the core its value depends on the degree of saturation of the iron. The effective length of the magnetic path is l_g + (l_c/μ), where μ is the permeability for the steady or d-c component of flux.

Reactor design is, to a large extent, the proportioning of values of air gap and magnetic path length divided by permeability. If the air gap is relatively large, the reactor inductance is not much affected by changes in μ; it is then called a linear reactor. If the air gap is small, changes in μ due to current or voltage variations cause inductance to vary; then the reactor is non-linear.

When direct current flows in an iron-core reactor, a fixed magnetizing force H_dc is maintained in the core. This is shown in Fig. 64 as the vertical line H_dc to the right of zero H in a typical a-c hysteresis loop, the upper half DB_mD' of which corresponds to that in Fig. 21. Increment ΔH of a-c magnetization, superposed on H_dc, causes flux density increment ΔB, with permeability μ_Δ equal to the slope of dotted line AB_m. ΔB is twice the peak a-c induction B_ac. It will be recalled from Fig. 19 that the normal induction curve OB_m is the locus of the end points of a series of successively smaller major hysteresis loops. Since the top of the minor loop always follows the left side of a major loop, as H_dc is reduced in successive steps the upper ends of corresponding minor loops terminate on the normal induction curve.

Dotted-line slopes of a series of minor loops are shown in Fig. 64, the midpoints of which are C, C', C", and C'".

Fig. 64. Incremental permeability with different amounts of d-c magnetization.

Increment of induction ΔB is the same for each minor loop. It will be seen that the width of the loop ΔH is smaller, and hence ma is greater, as H_dc is made smaller.

Midpoints C, C', etc., form the locus of d-c induction. The slope of straight line OC is the d-c permeability for core magnetization H_dc. It is much greater than the slope of AB_m. Hence incremental permeability is much smaller than d-c permeability. This is true in varying degree for all the minor loops. The smaller ΔB is, the less the slope of a minor loop becomes, and consequently the smaller the value of incremental permeability μ_Δ. The curve in Fig. 65 marked μ is the normal permeability of 4% silicon steel for steady values of flux, in other words, for the d-c flux in the core.

Fig. 65. Normal and incremental permeability of 4% silicon steel.

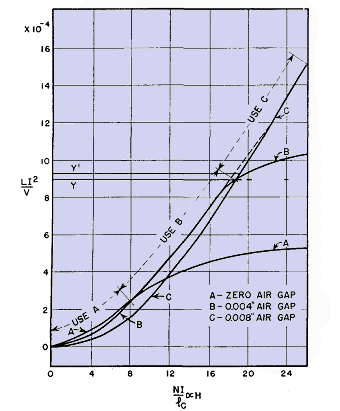
It is 4 to 20 times as great as the incremental permeability μ_Δ for a small alternating flux superposed upon the d-c flux. The ratio of μ to μ_Δ gradually increases as d-c flux density increases.

Because of the low value of μ_Δ for minute alternating voltages, the effective length of magnetic path l_g + (I_c/μ_Δ) is considerably greater for alternating than for steady flux. But the inductance varies inversely as the length of a-c flux path. If, therefore, the incremental permeability is small enough to make l_c/μ_Δlarge compared to l_g, it follows that small variations in l_g do not affect the inductance much. For this reason the exact value of the air gap is not important with small alternating voltages.

Reactor size, with a given voltage and ratio of inductance to resistance, is proportional to the stored energy LI². For the design of reactors carrying direct current, that is, the selection of the right number of turns, air gap, and so on, a simple method was originated by C. R. Hanna.⁽¹⁾ By this method, magnetic data are reduced to curves such as Fig. 66, plotted between LI²/V and NI/l_c from which reactors can be designed directly. The various symbols in the coordinates are:

L = a-c inductance in henrys

A_c = cross section of core in square inches

I = direct current in amperes

V = volume of iron core in cubic inches = A_cl_c (see Fig. 57 for core dimensions)

l_c = length of core in inches

N = number of turns in winding

l_g = air gap in inches

Fig. 66. Reactor energy per unit volume versus ampere-turns per inch of core.

Each curve of Fig. 66 is the envelope of a family of fixed air-gap curves such as those shown in Fig. 67.

Fig. 67. Fixed air-gap curves. For Bdc « Bac, air gap is not critical.

These curves are plots of data based upon a constant small a-c flux (10 gauss) in the core but a large and variable d-c flux. Each curve has a region of optimum usefulness, beyond which saturation sets in and its place is taken by a succeeding curve having a larger air gap. A curve tangent to the series of fixed air-gap curves is plotted as in Fig. 66, and the regions of optimum usefulness are indicated by the scale l_g/l_c. Hence Fig. 66 is determined mainly by the d-c flux conditions in the core and represents the most LI² for a given amount of material.

Figure 67 illustrates how the exact value of air gap is of little consequence in the final result. The dotted curve connecting B and C is for a 6-mil gap. Point Y' represents the maximum inductance that could be obtained from a given core for NI/l_c = 19. Point Y is the inductance obtained if a gap of either 4 or 8 mils is used. The difference in inductance between Y and Y' is 4 per cent, for a difference in air gap of 33 per cent.

An example will show how easy it is to make a reactor according to this method.

(1)	Design of Reactances and Transformers Which Carry Direct Current," by C. R. Hanna, J. AIEE, 46, 128 (February, 1927).