Harmonic Distortion

Audio response may be good according to Figs. 109, 110, 111, and 113, but at the same time the output may be badly distorted because of changes in load impedance or phase angle.

Fig. 112. Audio amplifier. Audio transformers are inverted on chassis at left. Power supply is at right.

Fig. 113. High-frequency response of step-down transformers.

This possibility is considered here for the case in which the load impedance is twice the source impedance.

The phase angle of the equivalent circuits of Figs. 107 (a) and (e) is found by taking the angle whose tangent is the ratio of imaginary to real components of the total circuit impedance in each case.

Fig. 114. Variation of amplifier phase angle at low frequencies.

This angle is plotted in Figs. 114 and 115 for the low- and high-frequency ranges, respectively, with the same abscissas as in Figs. 108 and 110.

Fig. 115. Variation of amplifier phase angle at high frequencies.

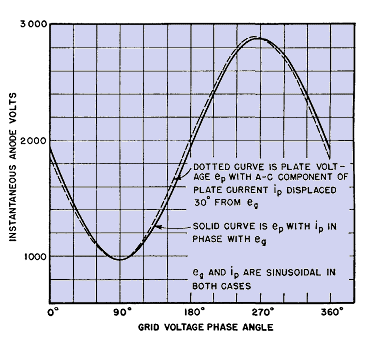
It is the angle between the voltage E₁ and the current entering the equivalent circuits of Figs. 107(c) and (e) and therefore represents the angle between a-c grid voltage and plate current. Positive angle indicates lagging plate current.

The phase angle exhibited by a transformer over the range considered in Figs. 114 and 115 does not exceed 30°, whereas for the most favorable curve in Fig. 115 (B = 1.0) it does not exceed 15°. To study the effect of phase angle alone upon distortion, the light load of 8,800 ohms is plotted upon the plate characteristics of triode type 851 in Fig. 116. The result is a sine wave of plate voltage. If the phase angle between grid voltage and plate current waves is then arbitrarily made 30°, as in Table XII, the elliptical load curve obtains.

Table XII. 851 Triode Operation with 8,800-Ohm 30° Phase Angle Load

θ (deg)	ec	iB	eB
0	- 60	0.245	1850
30	- 33	0.300	1400
60	- 13	0.355	1080
90	- 6	0.395	960
120	- 13	0.410	1150
150	- 33	0.395	1520
180	- 60	0.355	2000
210	- 87	0.300	2460
240	-107	0.245	2790
270	-114	0.205	2880
300	-107	0.190	2720
330	- 87	0.205	2350
360	- 60	0.245	1850

The wave of plate voltage is plotted for both zero and 30° phase angle in Fig. 117.

Fig. 116. Triode type 851 with reactive load.

Fig. 117. Plate voltage wave forms with zero and 30° phase angles.

These wave forms indicate that the phase angle encountered in audio transformers does not of itself introduce much distortion in a lightly loaded triode.

The influence of load impedance on distortion will be considered next. In Fig. 107(c) the load impedance, to the right of the dotted line, is

[65]

Hence

[66]

Equation 66 is plotted in Fig. 118.

Fig. 118. Variation of load impedance with transformer characteristics at low frequencies.

It shows the change in load Z from its median-frequency value R₂, as the frequency is lowered. Abscissas are X_N/R₂ instead of X_N/R₁ as in Fig. 108.

For the higher audio frequencies, the load impedance at the right of the dotted line in Fig. 107(e) is

[67]

If we let X_c/R₂ = D at frequency f_r, then, at any frequency f, X_c/R₂ = Df_r/f. If this substitution is made in equation 67 and also if X_L/X_c = f²f_r²,

[67a]

Equation 67a is plotted in Fig. 119 for several values of D. The impedance varies widely from its median-frequency value, especially at lower values of D.

Fig. 119. Variation of load impedance with transformer characteristics at high frequencies.

From Figs. 118 and 119 it is possible to compare the change in impedance with the frequency response curves in Figs. 108 and 110. When this comparison is made it should be remembered that B = 2D for the triode conditions assumed here. If the amplifier response is allowed to fall off 1.0 db at the lowest frequency, the corresponding value of X_N/R₁. from Fig. 108 is 1.3. This means that X_N/R₂ is 0.65. The corresponding load impedance in Fig. 118 is only 0.55 of its median-frequency value. Likewise, for 0.5-db droop of the frequency characteristic, the load impedance falls to 0.7R₂, whereas for a good load impedance of 0.9R₂ the frequency characteristic can fall off only 0.1 db. It is thus evident that load impedance may vary widely even with comparatively flat frequency characteristics.

At high audio frequencies the divergences are still greater. Suppose, for example, that a transformer has been designed so that X_c/R₁ is 1.0 at f_r (that is, B = 1.0 in Fig. 110). Suppose further that the highest audio frequency at which the transformer operates is 0.75f_r. The amplifier then has a relatively flat characteristic, with a slight rise near its upper limit of frequency. In Fig. 119, the curve corresponding to B = 1.0 is marked D = 0.5, for which at 0.75f_r the load impedance has dropped to 32 per cent of R₂, an extremely poor match for the tube.

It might be thought that, since 0.75f_r is the upper frequency limit, the harmonics resulting from the low value of load impedance would not be amplified, and no harm would be done. But at the frequency 0.375f_r, whose second harmonic would be amplified, the load impedance is only 0.69R₂.

Between 0.375f_r and 0.75f_r (over half of the amplifier frequency range) the load impedance gradually drops from 0.69R₂ to 0.327R₂. Thus distortion is large over a wide frequency range. It would be much better to design the transformer so that B = 2.0; the change in impedance is much less, and the rise in response is slight.

To ascertain how much distortion these low load impedances produce, a series of loads was plotted in Fig. 116 on 851 plate characteristics: 100, 70, and 50 per cent of the class A UPO value of twice the plate resistance (3,100, 2,200, and 1,550 ohms, respectively). The distortion is tabulated below for 54 volts grid swing.

Load	Percentage of 2nd Harmonic	Percentage of 3rd Harmonic	Plate Voltage Swing (Peak to Peak)
3100 ohms	4	1	1500
2200 ohms	10	4	1270
1550 ohms	19	6	1100

The plate voltage amplitude decrease with low impedance loads means that the combination of tube and transformer has a characteristic which droops instead of remaining flat as indicated by the curve B = 1.0 in Fig. 110.

This droop modifies the upper ends of the curves of Fig. 110. Although these curves were intended specifically for vacuum tubes, they were derived on the basis of a constant sinusoidal voltage in the source. Figure 119 demonstrates one important fact: For vacuum tubes operating into loads of twice the tube plate resistance, it is better to design transformers so that B = 2 or more. Then the output voltage and distortion are less affected by impedance variations at high frequencies. The actual frequency characteristics for triodes lie somewhere between the curves of Fig. 110 and the corresponding curves of Fig. 119.

Designing transformers for B ≥ 2.0 means keeping the effective capacitance lower, but the leakage inductance may be proportionately greater than for transformers having B = 1.0.

Variations of load impedance at high frequency shown in Fig. 119 are for step-up transformers. Similar variations for step-down transformers may be found from equation 68.

[68]

Equation 68 is plotted in Fig. 120.

Fig. 120. Step-down transformer impedance at high frequencies.

Impedance rises to peaks in the vicinity of f_r, in contrast to the valleys in Fig. 119. For the same variation of impedance, the frequency range is greater for step-down transformers, especially with values of D = 0.5 and 0.7.

Besides the harmonic distortion caused by variations in load impedance, at low frequencies additional distortion is caused by nonlinear magnetizing current. If a transformer is connected to a 60-cycle supply line, the no-load current contains large harmonics, but the voltage wave form remains sinusoidal because the line impedance is low. But if distorted magnetizing current is drawn from an amplifier tube, the plate resistance is high enough to produce a distorted voltage wave form across the transformer primary winding, caused mainly by the third harmonic. If the harmonic current amplitude I_H in the magnetizing current is found by connecting the transformer across a low-impedance source, the amplitude of harmonic voltage appearing in the output with a higher-impedance source is

[69]

where

E_h = harmonic voltage amplitude
E_f = fundamental voltage amplitude
I_H = harmonic current amplitude
I_f = fundamental current amplitude
R = R₁R₂/(R₁ + R₂). R₁, R₂, and X_N are as shown in Fig. 107(c).⁽¹⁾

If flux density is below the knee of the saturation curve, and if X_N = 3R₂ at the lowest operating frequency, the harmonic amplitude is less than 5 per cent. An air gap in the core reduces this figure. Table XIII gives typical harmonic currents for silicon steel.

Table XIII. Typical Silicon-Steel Magnetizing Current Harmonic Components with Zero Impedance Source

Bm Gauss	Percentage of 3rd Harmonic	Percentage of 5th Harmonic
100	4	1
500	7	1.5
1,000	9	2.0
3,000	15	2.5
5,000	20	3.0
10,000	30	5.0

Output voltage distortion may be analyzed to find harmonic content by the usual Fourier method. Several simplifications have been devised to reduce the labor and increase accuracy.⁽²⁾ In general, if the recommended tube load impedances are maintained, harmonic percentages will be as given in the tube manuals. If other load impedances obtain at some frequencies, to predict the harmonic output requires harmonic analysis.

(1)	For a discussion of equation 69 and magnetizing currents in general, see "Harmonic Distortion in Audio-Frequency Transformers," by N. Partridge, Wireless Engr., 19 (September, October, and November, 1942).
(2)	For example, "Graphical Harmonic Analysis," by J. A. Hutcheson, Electronics, 9, 16 (January, 1936).