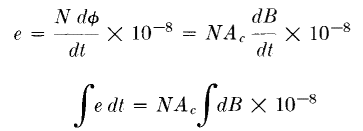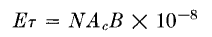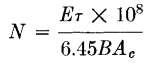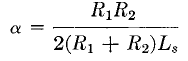Design of Pulse Transformers

(A) Requirements. The performance of a pulse transformer is usually specified by the following:

• Pulse voltage.
• Voltage ratio.
• Pulse duration.
• Repetition rate.
• Power or impedance level.
• Slope of front.
• Droop on top.
• Amount of backswing permissible.
• Type of load.

Design data for insuring that these requirements are met are provided in the foregoing sections, in several sets of curves. Below are outlined the steps followed in utilizing these curves for design purposes.

(B) Start of Design. The first step in beginning a design is to choose a core. It is helpful if some previous design exists which is close in rating to the transformer about to be designed.

After choosing the core to be used, the designer must next figure the number of turns. In pulse transformers intended for high voltages, the limiting factor is usually flux density. If so, the number of turns may be derived as follows, for unidirectional pulses:

[138]

For a square wave, e = E and

or

[139]

where

E = pulse voltage

τ = pulse duration in seconds

B = allowable flux density in gauss

A_c = core section in square inches

N = number of turns.

In many designs, the amount of droop or the backswing which can be tolerated at the end of the pulse determines the number of turns, because of their relation to the OCL of the transformer.

After the turns are determined, appropriate winding interleaving should be estimated and the leakage inductance and capacitance calculated.

With the leakage inductance and winding capacitance estimated, the front-end performance for linear loads can be found from Figs. 230 and 231. Likewise, from OCL and winding capacitance, the shapes of the top and trailing edge are found in Figs. 234 and 235. If performance from these curves is satisfactory and the coil fits the core, the design is completed.

(C) Final Calculations. Preliminary calculations may show too much slope on the front edge of the pulse (as often happens with new designs). Two damping factors R₁/2L_S and 1/2R₂C₂ contribute to the front-edge slope, and the preliminary calculations show which one is preponderant. Sometimes it is possible to increase leakage inductance or capacitance without increasing time constant T greatly, and this may be utilized in decreasing the slope.

If the front-edge slope is still too much after these adjustments, the core chosen is probably inadequate. Small core dimensions are desirable for low leakage inductance and winding capacitance. Small core area A_o may require too many turns to fit the core. These two considerations work against each other, so that the right choice of core is a problem in any design.

If the calculated front-edge slope is nearly good enough it may be improved by one of the following means:

• Change number of turns.
• Reduce core size.
• Change interleaving.
• Increase insulation thickness.
• Reduce insulation dielectric constant.

High capacitance is a common cause of poor performance and items (b) to (e) may often be changed to decrease the capacitance. It is sometimes possible to rearrange the circuit to better advantage and thereby make a deficient transformer acceptable. One illustration of this is the termination of a transmission line. Line termination resistance may be placed either on the primary or secondary side. If it is placed on the primary side there is usually a much improved front edge. Figure 231 does not show this improvement inasmuch as it was plotted for Fig. 229. For resistance on the primary side, the damping factor reduces to the single term

[140]

Improvement of the trailing-edge performance usually accompanies improvement of the front edge.

Core permeability is important because it requires fewer turns to obtain the necessary OCL with high-permeability core material. Permeability at the beginning of the trailing edge (point b', Fig. 236) is most important, for two reasons: the droop at this point depends on the OCL, so that for a given amount of droop the turns on the core are fixed; also, the normal permeability data apply to such points as b'. Flux density is chosen with two aims: it should be as high as possible for small size, but not so high as to result in excessive magnetizing current and backswing voltage.