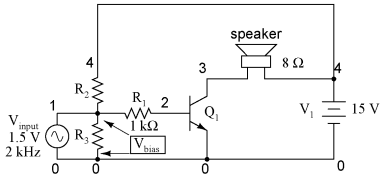
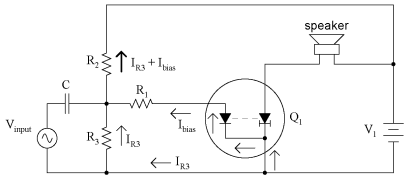
Practical Biasing Techniques

Now that we know a little more about the consequences of different DC bias voltage levels, it is time to investigate practical biasing techniques. So far, I've shown a small DC voltage source (battery) connected in series with the AC input signal to bias the amplifier for whatever desired class of operation. In real life, the connection of a precisely-calibrated battery to the input of an amplifier is simply not practical. Even if it were possible to customize a battery to produce just the right amount of voltage for any given bias requirement, that battery would not remain at its manufactured voltage indefinitely. Once it started to discharge and its output voltage drooped, the amplifier would begin to drift in the direction of class B operation.

Take this circuit, illustrated in the common-emitter section for a SPICE simulation, for instance:

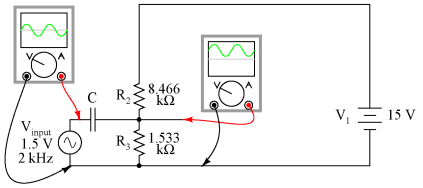
That 2.3 volt "V_bias" battery would not be practical to include in a real amplifier circuit. A far more practical method of obtaining bias voltage for this amplifier would be to develop the necessary 2.3 volts using a voltage divider network connected across the 15 volt battery. After all, the 15 volt battery is already there by necessity, and voltage divider circuits are very easy to design and build. Let's see how this might look:

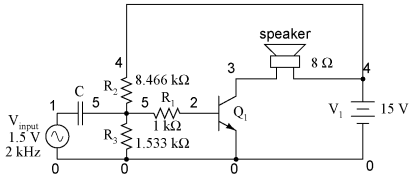
If we choose a pair of resistor values for R₂ and R₃ that will produce 2.3 volts across R₃ from a total of 15 volts (such as 8466 Ω for R₂ and 1533 Ω for R₃), we should have our desired value of 2.3 volts between base and emitter for biasing with no signal input. The only problem is, this circuit configuration places the AC input signal source directly in parallel with R₃ of our voltage divider. This is not acceptable, as the AC source will tend to overpower any DC voltage dropped across R₃. Parallel components must have the same voltage, so if an AC voltage source is directly connected across one resistor of a DC voltage divider, the AC source will "win" and there will be no DC bias voltage added to the signal.

One way to make this scheme work, although it may not be obvious why it will work, is to place a coupling capacitor between the AC voltage source and the voltage divider like this:

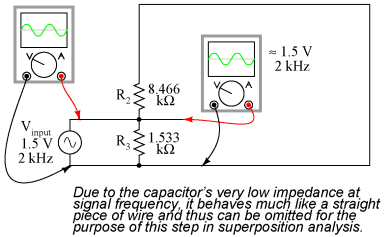
The capacitor forms a high-pass filter between the AC source and the DC voltage divider, passing almost all of the AC signal voltage on to the transistor while blocking all DC voltage from being shorted through the AC signal source. This makes much more sense if you understand the superposition theorem and how it works. According to superposition, any linear, bilateral circuit can be analyzed in a piecemeal fashion by only considering one power source at a time, then algebraically adding the effects of all power sources to find the final result. If we were to separate the capacitor and R₂R₃ voltage divider circuit from the rest of the amplifier, it might be easier to understand how this superposition of AC and DC would work.

With only the AC signal source in effect, and a capacitor with an arbitrarily low impedance at signal frequency, almost all the AC voltage appears across R₃:

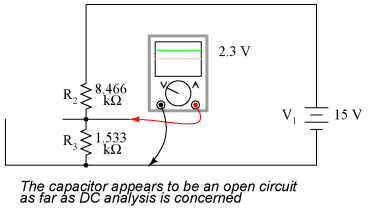
With only the DC source in effect, the capacitor appears to be an open circuit, and thus neither it nor the shorted AC signal source will have any effect on the operation of the R₂R₃ voltage divider:

Combining these two separate analyses, we get a superposition of (almost) 1.5 volts AC and 2.3 volts DC, ready to be connected to the base of the transistor:

Enough talk -- it's about time for a SPICE simulation of the whole amplifier circuit. I'll use a capacitor value of 100 μF to obtain an arbitrarily low (0.796 Ω) impedance at 2000 Hz:

voltage divider biasing
vinput 1 0 sin (0 1.5 2000 0 0)
c1 1 5 100u
r1 5 2 1k
r2 4 5 8466
r3 5 0 1533
q1 3 2 0 mod1
rspkr 3 4 8
v1 4 0 dc 15
.model mod1 npn
.tran 0.02m 0.78m
.plot tran v(1,0) i(v1)
.end

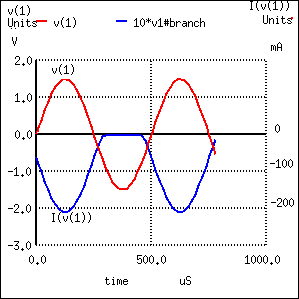
Notice that there is substantial distortion in the output waveform here: the sine wave is being clipped during most of the input signal's negative half-cycle. This tells us the transistor is entering into cutoff mode when it shouldn't (I'm assuming a goal of class A operation as before). Why is this? This new biasing technique should give us exactly the same amount of DC bias voltage as before, right?

With the capacitor and R₂R₃ resistor network unloaded, it will provide exactly 2.3 volts worth of DC bias. However, once we connect this network to the transistor, it is no longer unloaded. Current drawn through the base of the transistor will load the voltage divider, thus reducing the DC bias voltage available for the transistor. Using the diode-regulating diode transistor model to illustrate, the bias problem becomes evident:

A voltage divider's output depends not only on the size of its constituent resistors, but also on how much current is being divided away from it through a load. In this case, the base-emitter PN junction of the transistor is a load that decreases the DC voltage dropped across R₃, due to the fact that the bias current joins with R₃'s current to go through R₂, upsetting the divider ratio formerly set by the resistance values of R₂ and R₃. In order to obtain a DC bias voltage of 2.3 volts, the values of R₂ and/or R₃ must be adjusted to compensate for the effect of base current loading. In this case, we want to increase the DC voltage dropped across R₃, so we can lower the value of R₂, raise the value of R₃, or both.

voltage divider biasing
vinput 1 0 sin (0 1.5 2000 0 0)
c1 1 5 100u
r1 5 2 1k
r2 4 5 6k      <--- R2 decreased to 6 k ohms
r3 5 0 4k      <--- R3 increased to 4 k ohms
q1 3 2 0 mod1
rspkr 3 4 8
v1 4 0 dc 15
.model mod1 npn
.tran 0.02m 0.78m
.plot tran v(1,0) i(v1)
.end

As you can see, the new resistor values of 6 kΩ and 4 kΩ (R₂ and R₃, respectively) results in class A waveform reproduction, just the way we wanted.

Review

Class A operation is where an amplifier is biased so as to be in the active mode throughout the entire waveform cycle, thus faithfully reproducing the whole waveform. Class B operation is where an amplifier is biased so that only half of the input waveform gets reproduced: either the positive half or the negative half. The transistor spends half its time in the active mode and half its time cutoff. Complementary pairs of transistors running in class B operation are often used to deliver high power amplification in audio signal systems, each transistor of the pair handling a separate half of the waveform cycle. Class B operation delivers better power efficiency than a class A amplifier of similar output power. Class AB operation is where an amplifier is biased at a point somewhere between class A and class B. Class C operation is where an amplifier's bias forces it to amplify only a small portion of the waveform. A majority of the transistor's time is spent in cutoff mode. In order for there to be a complete waveform at the output, a resonant tank circuit is often used as a "flywheel" to maintain oscillations for a few cycles after each "kick" from the amplifier. Because the transistor is not conducting most of the time, power efficiencies are very high for a class C amplifier. Class D operation requires an advanced circuit design, and functions on the principle of representing instantaneous input signal amplitude by the duty cycle of a high-frequency squarewave. The output transistor(s) never operate in active mode, only cutoff and saturation. Thus, there is very little heat energy dissipated and energy efficiency is high. DC bias voltage on the input signal, necessary for certain classes of operation (especially class A and class C), may be obtained through the use of a voltage divider and coupling capacitor rather than a battery connected in series with the AC signal source.