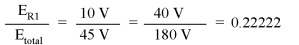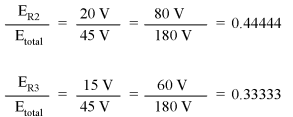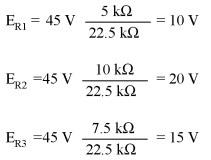| The ebook FEEE - Fundamentals of Electrical Engineering and Electronics is based on material originally written by T.R. Kuphaldt and various co-authors. For more information please read the copyright pages. |

|

Home  DC DC  Divider Circuits and Kirchhoff's Laws Divider Circuits and Kirchhoff's Laws  Voltage divider circuits Voltage divider circuits |
|






|
|
|
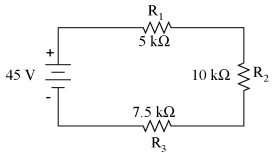
Voltage divider circuitsVoltage dividerLet's analyze a simple series circuit, determining the voltage drops across individual resistors:
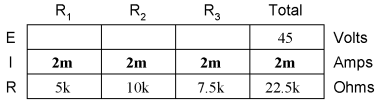
From the given values of individual resistances, we can determine a total circuit resistance, knowing that resistances add in series:
From here, we can use Ohm's Law (I=E/R) to determine the total current, which we know will be the same as each resistor current, currents being equal in all parts of a series circuit:
Now, knowing that the circuit current is 2 mA, we can use Ohm's Law (E=IR) to calculate voltage across each resistor:
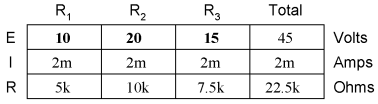
It should be apparent that the voltage drop across each resistor is proportional to its resistance, given that the current is the same through all resistors. Notice how the voltage across R2 is double that of the voltage across R1, just as the resistance of R2 is double that of R1. If we were to change the total voltage, we would find this proportionality of voltage drops remains constant:
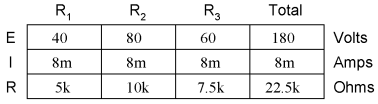
The voltage across R2 is still exactly twice that of R1's drop, despite the fact that the source voltage has changed. The proportionality of voltage drops (ratio of one to another) is strictly a function of resistance values. With a little more observation, it becomes apparent that the voltage drop across each resistor is also a fixed proportion of the supply voltage. The voltage across R1, for example, was 10 volts when the battery supply was 45 volts. When the battery voltage was increased to 180 volts (4 times as much), the voltage drop across R1 also increased by a factor of 4 (from 10 to 40 volts). The ratio between R1's voltage drop and total voltage, however, did not change:
Likewise, none of the other voltage drop ratios changed with the increased supply voltage either:
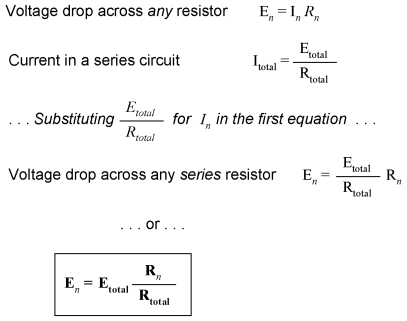
For this reason a series circuit is often called a voltage divider for its ability to proportion -- or divide -- the total voltage into fractional portions of constant ratio. With a little bit of algebra, we can derive a formula for determining series resistor voltage drop given nothing more than total voltage, individual resistance, and total resistance:
The ratio of individual resistance to total resistance is the same as the ratio of individual voltage drop to total supply voltage in a voltage divider circuit. This is known as the voltage divider formula, and it is a short-cut method for determining voltage drop in a series circuit without going through the current calculation(s) of Ohm's Law. Using this formula, we can re-analyze the example circuit's voltage drops in fewer steps:
Voltage dividers find wide application in electric meter circuits, where specific combinations of series resistors are used to "divide" a voltage into precise proportions as part of a voltage measurement device.
|
|
Home  DC DC  Divider Circuits and Kirchhoff's Laws Divider Circuits and Kirchhoff's Laws  Voltage divider circuits Voltage divider circuits |
|
Last Update: 2010-11-19