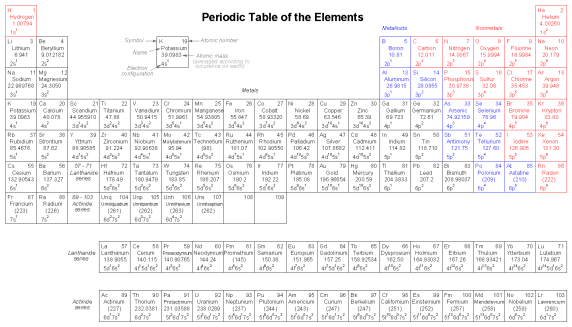
Pauli exclusion principle

The physicist Wolfgang Pauli developed a principle explaining the ordering of electrons in an atom according to these quantum numbers. His principle, called the Pauli exclusion principle, states that no two electrons in the same atom may occupy the exact same quantum states. That is, each electron in an atom has a unique set of quantum numbers. This limits the number of electrons that may occupy any given orbital, subshell, and shell.

Shown here is the electron arrangement for a hydrogen atom:

With one proton in the nucleus, it takes one electron to electrostatically balance the atom (the proton's positive electric charge exactly balanced by the electron's negative electric charge). This one electron resides in the lowest shell (n=1), the first subshell (l=0), in the only orbital (spatial orientation) of that subshell (m_l=0), with a spin value of 1/2. A common method of describing this organization is by listing the electrons according to their shells and subshells in a convention called spectroscopic notation. In this notation, the shell number is shown as an integer, the subshell as a letter (s,p,d,f), and the total number of electrons in the subshell (all orbitals, all spins) as a superscript. Thus, hydrogen, with its lone electron residing in the base level, is described as 1s¹.

Proceeding to the next atom (in order of atomic number), we have the element helium:

A helium atom has two protons in the nucleus, and this necessitates two electrons to balance the double-positive electric charge. Since two electrons -- one with spin=1/2 and the other with spin=-1/2 -- fit into one orbital, the electron configuration of helium requires no additional subshells or shells to hold the second electron.

However, an atom requiring three or more electrons will require additional subshells to hold all electrons, since only two electrons will fit into the lowest shell (n=1). Consider the next atom in the sequence of increasing atomic numbers, lithium:

An atom of lithium uses a fraction of the L shell's (n=2) capacity. This shell actually has a total capacity of eight electrons (maximum shell capacity = 2n² electrons). If we examine the organization of the atom with a completely filled L shell, we will see how all combinations of subshells, orbitals, and spins are occupied by electrons:

Often, when the spectroscopic notation is given for an atom, any shells that are completely filled are omitted, and the unfilled, or the highest-level filled shell, is denoted. For example, the element neon (shown in the previous illustration), which has two completely filled shells, may be spectroscopically described simply as 2p⁶ rather than 1s²2s²2p⁶. Lithium, with its K shell completely filled and a solitary electron in the L shell, may be described simply as 2s¹ rather than 1s²2s¹.

The omission of completely filled, lower-level shells is not just a notational convenience. It also illustrates a basic principle of chemistry: that the chemical behavior of an element is primarily determined by its unfilled shells. Both hydrogen and lithium have a single electron in their outermost shells (1s¹ and 2s¹, respectively), and this gives the two elements some similar properties. Both are highly reactive, and reactive in much the same way (bonding to similar elements in similar modes). It matters little that lithium has a completely filled K shell underneath its almost-vacant L shell: the unfilled L shell is the shell that determines its chemical behavior.

Elements having completely filled outer shells are classified as noble, and are distinguished by almost complete non-reactivity with other elements. These elements used to be classified as inert, when it was thought that these were completely unreactive, but are now known to form compounds with other elements under specific conditions.

Since elements with identical electron configurations in their outermost shell(s) exhibit similar chemical properties, Dimitri Mendeleev organized the different elements in a table accordingly. Such a table is known as a periodic table of the elements, and modern tables follow this general form in Figure below.

Periodic table of chemical elements.

Dmitri Mendeleev, a Russian chemist, was the first to develop a periodic table of the elements. Although Mendeleev organized his table according to atomic mass rather than atomic number, and produced a table that was not quite as useful as modern periodic tables, his development stands as an excellent example of scientific proof. Seeing the patterns of periodicity (similar chemical properties according to atomic mass), Mendeleev hypothesized that all elements should fit into this ordered scheme. When he discovered “empty” spots in the table, he followed the logic of the existing order and hypothesized the existence of heretofore undiscovered elements. The subsequent discovery of those elements granted scientific legitimacy to Mendeleev's hypothesis, further discoveries leading to the form of the periodic table we use today.

This is how science should work: hypotheses followed to their logical conclusions, and accepted, modified, or rejected as determined by the agreement of experimental data to those conclusions. Any fool may formulate a hypothesis after-the-fact to explain existing experimental data, and many do. What sets a scientific hypothesis apart from post hoc speculation is the prediction of future experimental data yet uncollected, and the possibility of disproof as a result of that data. To boldly follow a hypothesis to its logical conclusion(s) and dare to predict the results of future experiments is not a dogmatic leap of faith, but rather a public test of that hypothesis, open to challenge from anyone able to produce contradictory data. In other words, scientific hypotheses are always“risky” due to the claim to predict the results of experiments not yet conducted, and are therefore susceptible to disproof if the experiments do not turn out as predicted. Thus, if a hypothesis successfully predicts the results of repeated experiments, its falsehood is disproven.

Quantum mechanics, first as a hypothesis and later as a theory, has proven to be extremely successful in predicting experimental results, hence the high degree of scientific confidence placed in it. Many scientists have reason to believe that it is an incomplete theory, though, as its predictions hold true more at micro physical scales than at macroscopic dimensions, but nevertheless it is a tremendously useful theory in explaining and predicting the interactions of particles and atoms.

As you have already seen in this chapter, quantum physics is essential in describing and predicting many different phenomena. In the next section, we will see its significance in the electrical conductivity of solid substances, including semiconductors. Simply put, nothing in chemistry or solid-state physics makes sense within the popular theoretical framework of electrons existing as discrete chunks of matter, whirling around atomic nuclei like miniature satellites. It is when electrons are viewed as “wavefunctions” existing in definite, discrete states that the regular and periodic behavior of matter can be explained.

Review

Electrons in atoms exist in “clouds” of distributed probability, not as discrete chunks of matter orbiting the nucleus like tiny satellites, as common illustrations of atoms show. Individual electrons around an atomic nucleus seek unique “states,” described by four quantum numbers: the Principal Quantum Number, known as the shell; the Angular Momentum Quantum Number, known as the subshell; the Magnetic Quantum Number, describing the orbital (subshell orientation); and the Spin Quantum Number, or simply spin. These states are quantized, meaning that no “in-between” conditions exist for an electron other than those states that fit into the quantum numbering scheme. The Principal Quantum Number (n) describes the basic level or shell that an electron resides in. The larger this number, the greater radius the electron cloud has from the atom's nucleus, and the greater than electron's energy. Principal quantum numbers are whole numbers (positive integers). The Angular Momentum Quantum Number (l) describes the shape of the electron cloud within a particular shell or level, and is often known as the “subshell.” There are as many subshells (electron cloud shapes) in any given shell as that shell's principal quantum number. Angular momentum quantum numbers are positive integers beginning at zero and ending at one less than the principal quantum number (n-1). The Magnetic Quantum Number (ml) describes which orientation a subshell (electron cloud shape) has. Subshells may assume as many different orientations as the subshell number (l) plus 1, and each unique orientation is called an orbital. These numbers are integers ranging from the negative value of the subshell number (l) through 0 to the positive value of the subshell number. The Spin Quantum Number (ms) describes another property of an electron, and may be a value of +1/2 or -1/2. Pauli's Exclusion Principle says that no two electrons in an atom may share the exact same set of quantum numbers. Therefore, no more than two electrons may occupy each orbital (spin=1/2 and spin=-1/2), 2l+1 orbitals in every subshell, and n subshells in every shell, and no more. Spectroscopic notation is a convention for denoting the electron configuration of an atom. Shells are shown as whole numbers, followed by subshell letters (s,p,d,f), with superscripted numbers totaling the number of electrons residing in each respective subshell. An atom's chemical behavior is solely determined by the electrons in the unfilled shells. Low-level shells that are completely filled have little or no effect on the chemical bonding characteristics of elements. Elements with completely filled electron shells are almost entirely unreactive, and are called noble (formerly known as inert).