| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Physical Chemistry Physical Chemistry  Equilibrium and the Second Law of Thermodynamics Equilibrium and the Second Law of Thermodynamics  Reaction Equilibrium Reaction Equilibrium |
|||






|
|||
Reaction EquilibriumAuthor: John Hutchinson
Having developed a thermodynamic understanding of phase equilibrium, it proves to be even more useful to examine the thermodynamic description of reaction equilibrium to understand why the reactants and products come to equilibrium at the specific values that are observed. Recall that ΔG=ΔH-TΔS<0 for a spontaneous process, and ΔG=ΔH-TΔS=0 at equilibrium. From these relations, we would predict that most (but not all) exothermic processes with ΔH<0 are spontaneous, because all such processes increase the entropy of the surroundings when they occur. Similarly, we would predict that most (but not all) processes with ΔS>0 are spontaneous. We try applying these conclusions to synthesis of ammonia
at 298K, for which we find that ΔS° = -198 J/molK. Note that ΔS°<0 because the reaction reduces the total number of gas molecules during ammonia synthesis, thus reducing W, the number of ways of arranging the atoms in these molecules. ΔS°<0 suggests that equation 6 should not occur at all. However, ΔH° = -92.2 kJ/mol. Overall, we find that ΔG° = -33.0 kJ/mol at 298K, which according to equation 3 suggests that equation 6 is spontaneous. Given this analysis, we are now pressed to ask, if equation 6 is predicted to be spontaneous, why does the reaction come to equilibrium without fully consuming all of the reactants? The answer lies in a more careful examination of the values given: ΔS°, ΔH°, and ΔG° are the values for this reaction at standard conditions, which means that all of the gases in the reactants and products are taken to be at 1 atm pressure. Thus, the fact that ΔG°<0 for equation 6 at standard conditions means that, if all three gases are present at 1 atm pressure, the reaction will spontaneously produce an increase in the amount of NH3. Note that this will reduce the pressure of the N2 and H2 and increase the pressure of the NH3. This changes the value of ΔS and thus of ΔG, because as we already know the entropies of all three gases depend on their pressures. As the pressure of NH3 increases, its entropy decreases, and as the pressures of the reactants gases decrease, their entropies increase. The result is that ΔS becomes increasingly negative. The reaction creates more NH3 until the value of ΔS is sufficiently negative that ΔG = ΔH-TΔS = 0. From this analysis, we can say by looking at ΔS°, ΔH°, and ΔG° that, since ΔG°<0 for equation 6, reaction equilibrium results in production of more product and less reactant than at standard conditions. Moreover, the more negative ΔG° is, the more strongly favored are the products over the reactants at equilibrium. By contrast, the more positive ΔG° is, the more strongly favored are the reactants over the products at equilibrium.
|
|||
Home  Physical Chemistry Physical Chemistry  Equilibrium and the Second Law of Thermodynamics Equilibrium and the Second Law of Thermodynamics  Reaction Equilibrium Reaction Equilibrium |
|||
Last Update: 2011-02-16


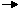 2 NH3 (g)
2 NH3 (g)