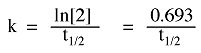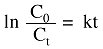Half Life

Author: Andrew R. Barron

It is interesting to note that there are no stable atoms with an atomic number greater than 83 (bismuth). The more massive atoms only exist because certain isotopes are very long lived and therefore on a normal time scale of years appear stable. Thus, uranium-238, uranium-232 and thorium-232 are very long-lived isotopes, while technetium does not have any stable isotopes.

Since unstable isotopes decay (via either α or β decay) we need a way to express the relative stability of isotopes or the time for radioactive decay. This is expressed by an isotopes half life (t_1/2). Empirical observation shows that the number of atoms of a radioactive element that disintegrates per unit time is a constant fraction of the total number of atoms.

Plot of the number of atoms of a radioactive element that disintegrates per unit time as a function of time.

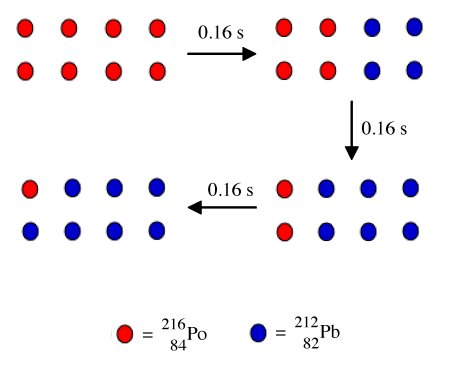
Based upon this the time required for ¹/₂ of the atoms of a radioactive element (X) to decay to a daughter element (Y) is defined as the half life. For example, polonium-216 decays to lead-206 with a half life of 0.16 seconds. Thus, as shown in the figure below, a sample of eight polonium-216 decays in 0.16 s to mixture of four lead-206 atoms and a residual of four polonium-216. After a further 0.16 s two of the remaining polonium-216 decay to lead-206, then in another 0.16 s one of the two remaining polonium-216 atoms decay to a lead-206 atom.

Schematic representation of the half life in the radioactive decay of polonium-216.

The following table shows selected isotopes and their half life:

Isotope	Half life
Cerium-142	5 x 1015 years
Radium-226	1590 years
Radon-222	3.82 days
Polonium-216	0.16 s

The rate of radioactive decay can be expressed as a rate constant (k):

[1]

The relation of the initial concentration (C₀) and the concentration at time t (C_t) can be expressed by the following:

[2]

It should be noted that

Using these equations the rate constant (k) can be calculated for a particular isotope. For example, colbolt-60 that is used in cancer therapy, decays to nickel-60 with loss of a β particle with a half life of 5.2 years:

Using Equation 1,

As an alternative knowing the rate constant we can calculate the fraction or percentage of cobalt-60 isotope that will remain in 15 years. From Equation 2,

The fraction remaining after 15 years is therefore determined as follows:

Thus, 14% of a sample of colbalt-60 isotope remains after 15 years.