| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Physical Chemistry Physical Chemistry  Phase Equilibrium and Intermolecular Interactions Phase Equilibrium and Intermolecular Interactions  Gas-Liquid Phase Transitions Gas-Liquid Phase Transitions |
|||||||
| See also: Phase Equilibrium, Vapor Pressure of a Liquid | |||||||






|
|||||||
Gas-Liquid Phase TransitionsAuthor: John Hutchinson
We begin by returning to our observations of Charles' Law. Recall that we trap an amount of gas in a cylinder fitted with a piston, and we apply a fixed pressure to the piston. We vary the temperature of the gas, and since the pressure applied to the piston is constant, the piston moves to maintain a constant pressure of the trapped gas. At each temperature, we then measure the volume of the gas. From our previous observations, we know that the volume of the gas is proportional to the absolute temperature in degrees Kelvin. Thus a graph of volume versus absolute temperature is a straight line, which can be extrapolated to zero volume at 0K.
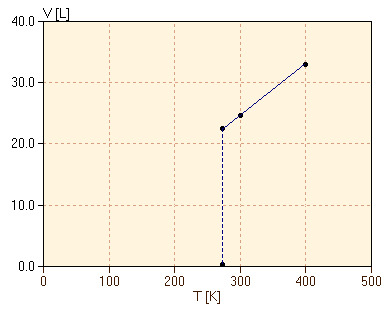
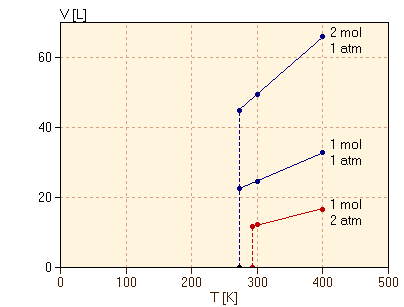
Consider, then, trying to measure the volume for lower and lower temperatures to follow the graph. To be specific, we take exactly 1.00 mol of butane C4H10 at 1 atm pressure. As we lower the temperature from 400K to 300K, we observe the expected proportional decrease in the volume from 32.8L to 24.6L and this proportionality works very well for temperatures just slightly above 272.6K, where the volume is 22.4L. However, when we reach 272.6K, the volume of the butane drops very abruptly, falling to about 0.097L at temperatures just slightly below 272.6K. This is less than one-half of one percent of the previous volume! The striking change in volume is shown in the graph as a vertical line at 272.6K. This dramatic change in physical properties at one temperature is referred to as a phase transition. When cooling butane through the temperature 272.6K, the butane is abruptly converted at that temperature from one phase, gas, to another phase, liquid, with very different physical properties. If we reverse the process, starting with liquid butane at 1 atm pressure and temperature below 272.6K and then heating, we find that the butane remains entirely liquid for temperatures below 272.6K and then becomes entirely gas for temperatures above 272.6K. We refer to the temperature of the phase transition as the boiling point temperature. (We will discuss the phases present at the boiling point, rather than above and below that temperature, in another section.) We now consider how the phase transition depends on a variety of factors. First, we consider capturing 2.00 mol of butane in the cylinder initially, still at 1 atm pressure. The volume of 2.00 mol is twice that of 1.00 mol, by Avogadro's hypothesis. The proportional decrease in the volume of 2.00 mol of gas is shown in figure 2 along with the previous result for 1.00 mol. Note that the phase transition is observed to occur at exactly the same temperature, 272.6K, even though there is double the mass of butane.
Consider instead then varying the applied pressure. The result for cooling 1.00 mol of butane at a constant 2.00 atm pressure is also shown in figure 2. We observe the now familiar phase transition with a similar dramatic drop in volume. However, in this case, we find that the phase transition occurs at 293.2K, over 20K higher than at the lower pressure. Therefore, the temperature of the phase transition depends on the pressure applied. We can measure the boiling point temperature of butane as a function of the applied pressure, and this result is plotted here.
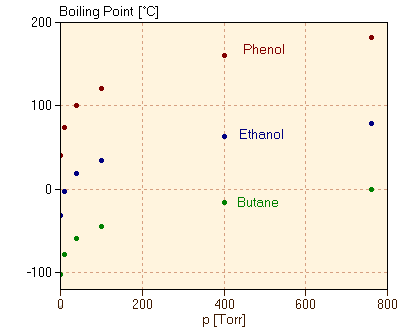
Finally, we consider varying the substance which we trap in the cylinder. In each case, we discover that the boiling point temperature depends on both what the substance is and on the applied pressure, but does not depend on the amount of the substance we trap. In figure 3, we have also plotted the boiling point as a function of the pressure for several substances. It is very clear that the boiling points for different substances can be very different from one another, although the variation of the boiling point with pressure looks similar from one substance to the next.
|
|||||||
Home  Physical Chemistry Physical Chemistry  Phase Equilibrium and Intermolecular Interactions Phase Equilibrium and Intermolecular Interactions  Gas-Liquid Phase Transitions Gas-Liquid Phase Transitions |
|||||||
Last Update: 2011-02-18