| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Atoms Atoms  Quantum Energy Levels In Atoms Quantum Energy Levels In Atoms  The Spectrum of Hydrogen The Spectrum of Hydrogen |
|||||






|
|||||
The Spectrum of HydrogenAuthor: John Hutchinson
To begin, we need to know a little about light. All forms of electromagnetic radiation travel as an oscillating wave, with an electric field component perpendicular to a magnetic field component. As a wave, the radiation can be characterized by its "wavelength", symbolized as λ, which is the distance between adjacent peaks in the wave. Different wavelengths correspond to different forms of electromagnetic radiation. For example, microwave radiation has wavelength in the range of 10-2 to 10-3 meters, whereas x-ray radiation has wavelength in the range 10-9 to 10-10 meters. Radiation which is visible to the human eye has wavelength in the very narrow range from 3.8
Radiation can also be characterized by the frequency of the electromagnetic wave, which is the number of peaks in the wave which pass a point in space per second. Frequency is symbolized by ν. The speed which light travels in a vacuum in the same for all forms of electromagnetic radiation, c=2.997
The longer the wavelength λ, the lower the frequency ν. This makes sense when we remember that light travels at a fixed speed. When the wavelength is longer, fewer peaks will pass a point in space in a second. From this equation, there is a specific relationship between frequency and wavelength, and either or both can be used to characterize the properties of radiation. With this background in hand, we can use our understanding of light to pursue more data about the energies of electrons in atoms. Ionization energies tell us how much energy is required to remove an electron from an atom, but do not tell what happens if an electron changes its energy in an atom. To analyze this, we need a means to measure the energies gained or lost by an atom. One way to do so is to analyze the "spectrum" of an atom, which is the set of frequencies of light emitted by the atom. Since hydrogen is the simplest atom, we analyze the hydrogen spectrum first. We find that, if we pass a current of electricity through a sample of hydrogen gas, light is emitted. Careful analysis shows that, although some of this light is emitted by H2 molecules, some of the light is also emitted by H atoms. Since light is a form of energy, then these H atoms must release energy supplied to them by the electrons in the current. Most importantly, if we pass the light emitted by the hydrogen gas sample through a prism, we can separate the colors as in a rainbow, each with a characteristic frequency. The resultant image of separated colors is called the spectrum of hydrogen. We find in this experiment that there are only four frequencies (four colors) of light in the emission that are visible. The most intense of the lines in the spectrum is bright red, but there are blue and violet lines. It turns out that there are also many other frequencies of light emitted which are invisible to the human eye. Careful observation and analysis reveals that every frequency in the hydrogen atom spectrum can be predicted by a very simple formula, called the Rydberg equation:
where R is the Rydberg constant (3.29
The atoms of all elements emit radiation when energized in an electric current, and as do all molecules of all compounds. However, we find that the specific frequencies of light emitted are characteristic of each atom or molecule. In other words, the spectrum of each element is unique to each element or compound. As a result, the spectrum of each substance can be used to identify that substance. (Note that the Rydberg equation tells us only the spectrum of hydrogen.) Our interest is in the fact that the radiation emitted by an atom tells us about the amounts of energy which can be released by an atom. For a hydrogen atom, for example, these changes in energy must correspond to the amounts of energy which the electrons inside the atom can gain or lose. At this point, we need to relate the frequency of radiation emitted by an atom to the amount of energy lost by the electron in the atom. We thus examine some observations about the energy of radiation.
|
|||||
Home  Atoms Atoms  Quantum Energy Levels In Atoms Quantum Energy Levels In Atoms  The Spectrum of Hydrogen The Spectrum of Hydrogen |
|||||
Last Update: 2011-02-16


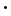 10-7 to 7.8
10-7 to 7.8