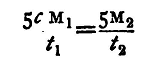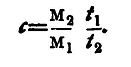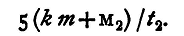The Method of Cooling

A known weight of the liquid is put into a copper vessel with a thermometer. This is hung by means of silk threads, like the calorimeter, inside another copper vessel which is closed by a lid with a cork in it supporting the thermometer. The exterior vessel is kept in a large bath of water at a known temperature, the bath being kept well stirred. It is intended to be maintained at the temperature of the room throughout the experiment; the bath is simply to ensure this. A small stirrer should pass through the cork which holds the thermometer, to keep the liquid well stirred. The outer surface of the inner vessel and the inner surface of the outer should be coated with lampblack.

The liquid is heated up to, say, 70° or 80°, and then put into the calorimeter.

Allow the liquid to cool, and note the intervals taken by it to cool, through, say, each successive degree. If the rate of cooling is too rapid to allow this to be done, note the intervals for each 5°. or 10°, and calculate from these observations the mean rate of cooling for the range experimented on, say from 70° to 30°.

Suppose we find that, on the average, it cools 3° in a minute. Then, if the liquid weigh 25 grammes and its specific heat be c, the quantity of heat which leaves it in one minute is 25 x 3 x c.

Now empty the liquid out from the calorimeter and perform a similar experiment with water instead. The water should fill the calorimeter to the same level, and be raised to the same temperature as the liquid previously used.

Let us now suppose that there are 32 grammes of water, and that the temperature of the water falls through 0.9 of a degree in one minute; thus the quantity of heat which escapes from the water per minute is 32 x 0.9 units.

The quantity of heat radiated from one surface at a given temperature to another at a constant lower temperature depends solely on the nature and material of the surfaces and the temperature of the warmer.⁽¹⁾

In the two experiments described above, the surfaces are of the same nature; thus the rate at which heat escapes must be the same for the two experiments at the same temperatures,

We can get the result required from the observations more quickly thus:

Observe the time it takes the temperature to fall, say, from 60° to 55° in the two cases; let it be t₁ minutes and t₂ minutes respectively.

Then the fall of temperature per minute in the two cases respectively is 5/t₁ and 5/t₂.

The amount of heat which is transferred in the first case

is 5cM₁/t₁, and in the second it is 5M₂/t₂, M₁, M₂ being the masses of the liquid and the water respectively. Thus

and

The effect of the vessel has hitherto been entirely neglected. Let k be its specific heat and m its mass, then in the first case the heat lost is

in the second it is

Thus

Instead of calculating the quantity km, we may find by experiment the water equivalent of the vessel and thermometer and use it instead of km.

Experiment. - Determine the specific heat of the given liquid.

Enter results thus:

Weight of calorimeter: 15.13 g
Weight of water:  10.94 g
Weight of liquid  13.20 g

Range of         Time of cooling of
Temperature    Liquid        Water     Specific heat uncorrected
70-65          115 s          130 s       0.733
65-60          125 s          140 s       0.734
6o-55          150 s          170 s       0.733
55-50          107 s          190 s       0.736

Mean specific heat (uncorrected for calorimeter) = 0.734
Correction for calorimeter =                      -0.013
Specific heat of liquid =                          0.721

(1)	See Garnett, Heat, ch. ix. Deschanel, Natural Philosophy p. 399, &c.