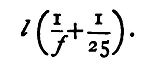Magnifying Power of a Lens or of a Microscope

A lens or microscope is used for the purpose of viewing objects whose distance from the eye is adjustable, and in such cases the magnifying power is taken to be the ratio of the angle subtended at the eye by the image as seen in the instrument to the angle subtended at the eye by the object when placed at the distance of most distinct vision (generally 25 cm). The instrument is supposed to be focussed so that the image appears to be at the distance of most distinct vision.

The method described for a telescope in §56 is applicable, with slight alteration, to the case of a lens or microscope. The instrument is focussed on a finely divided scale; one eye looks at the magnified image while the other looks at another scale placed so as to be 25 cm away from the eye, and to appear to coincide in position with the image of the first scale viewed through the instrument. Suppose the two scales are similarly graduated, and that x divisions of the magnified scale cover x divisions of the scale seen directly, then the magnifying power is X/x. If the two scales be not similarly divided - and it is often more convenient that they should not be so - a little consideration will show how the calculation is to be made. Thus, if the magnified scale be divided into m^ths of an inch, and the unmagnified one into n^ths, and if x divisions of the magnified scale cover x unmagnified divisions, then the magnified image of a length of x/m inches covers an unmagnified length of X/n inches, and the magnifying power is therefore mX/nx.

The following modification of the method gives the two images superposed when only one eye is used: Mount a camera-lucida prism so that its edge passes over the centre of the eye-lens of the microscope. Then half the pupil of the eye is illuminated by light coming through the microscope, and the other half by light reflected at right angles by the prism. If a scale be placed 25 cm. away from the prism, its image seen in the camera-lucida may be made to coincide in position with the image of the scale seen by the other half of the pupil through the microscope.

To make this experiment successful, attention must be paid to the illumination of the two scales. It must be remembered that magnifying the scale by the microscope reduces proportionately the brightness of the image. Thus the magnified scale should be as brightly illuminated as possible, and the reflected scale should be only feebly illuminated. It should also have a black screen behind it, to cut off the light from any bright object in the background.

A piece of plane unsilvered glass set at 45°, or a mirror with a small piece of the silvering removed, may be used instead of the camera lucida prism.

The magnifying power of a thin lens may be calculated approximately from its focal length. The eye being placed close to the lens, we may take angles subtended at the centre of the lens to be equal to angles subtended at the eye. Now a small object of length l placed at a distance of 25 cm subtends an angle whose measure may be taken to be l/25. When the lens is interposed the image is to be at a distance of 25 cm, and the distance between the object and eye must be altered; the object will therefore be at a distance u where

The angle subtended by the image is similarly measured by its length divided by 25, and this is equal to l/μ, or

Thus the magnifying power is

or

A microscope with a micrometer scale in the eye-piece is sometimes used to measure small distances. We may therefore be required to determine what actual length corresponds, when magnified, to one of the divisions of the micrometer scale in the eye-piece.

For this purpose place below the object-glass a scale divided, say, to tenths of a millimetre, and note the number of divisions of the eye-piece scale which are covered by one division of the object scale seen through the microscope; let it be a. Then each division of the eye-piece scale corresponds clearly to 1/a of one-tenth of one millimetre, and an object seen through the microscope which appears to cover b of these eye-piece divisions is in length equal to b/a of one-tenth of a millimetre.

If we happen to know the value of the divisions of the eye-piece scale we can get from this the magnifying power of the object-glass itself, in the case in which the microscope is fitted with a Ramsden's or positive eye-piece, and thence, on determining the magnifying power of the eye-piece, find that of the whole microscope. For if m₁ be the magnifying power of the object-glass, m₂ that of the eye-piece, then that of the whole microscope is m₁ x m₂.

Thus, if the eye-piece scale is itself divided to tenths of millimetres, since one-tenth of a millimetre of the object scale appears to cover a tenths of a millimetre of the eyepiece scale, the magnifying power of the object-glass is a.

If, on the other hand, the microscope is fitted with a Huyghens or negative eye-piece, then the eye-piece scale is viewed through only the second or eye lens of the eyepiece, while the image of the object scale, which appears to coincide with it, is that formed by refraction at the object-glass and the first or field lens of the eye-piece; the magnifying power determined as above is that of the combination of object-glass and field lens. To determine the magnifying power for the whole microscope, in this case we must find that of the eye-lens and multiply the two together.

It should be noticed that the magnifying power of a microscope depends on the relative position of the object-glass and eye-piece. Accordingly, if the value of the magnifying power is to be used in subsequent experiments, the focussing of the object viewed must be accomplished by moving the whole instrument.

Experiment. - Determine by both methods the magnifying power of the given microscope.

Enter the results thus:

First method. - Scale viewed through microscope graduated to half-millimetres. Scale viewed directly graduated to millimetres.

Three divisions of scale seen through microscope cover 129 of scale seen directly.

Magnifying power = 129/(3/2) = 86.

Second method. - One division of eye-piece scale = 0.5 mm. Three divisions of scale viewed cover 14.57 divisions of eyepiece scale.

Magnifying power of eye-piece 18.

Magnifying power of microscope = 14.58/3*18 = 87.4.