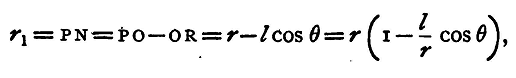| Practical Physics is a free textbook on basic laboratory physics. See the editorial for more information.... |

|

Home  Magnetism Magnetism  Magnetic Potential due to a Solenoidal Magnet Magnetic Potential due to a Solenoidal Magnet |
|






|
|
Magnetic Potential due to a Solenoidal Magnet
We have seen that if P be a point at distances r1, r2 from the north and south poles, N, S, respectively, of a solenoidal magnet NOS (fig. 44) of strength m, the magnetic potential at P is
Draw NR, ST perpendicular to PO or PO produced, and suppose that OP is so great compared with ON that we may neglect the square and higher powers of the ratio of ON/OP. Then PRN is a right angle, and PNR differs very little from a right angle, for ON is small compared with OP, so that PxN = PR very approximately, and similarly PS = PT. Also OR = OT = ONcos(PON) = lcosθ. Thus
and
and, if v denote the magnetic potential at P, we have
But we are to neglect terms involving l2/r2, etc.; thus we may put
if M be the moment of the magnet. We shall see next how to obtain from this expression the magnetic force at P.
|
|
Home  Magnetism Magnetism  Magnetic Potential due to a Solenoidal Magnet Magnetic Potential due to a Solenoidal Magnet |
|
Last Update: 2011-03-16



 We will now put this expression into another and more useful form, to which it is for our purposes practically equivalent. Let O, the middle point of the line NS, be the centre of the magnet; let OP=r, ON = OS = l, so that 2l is the length of the magnet, and let the angle between the magnetic axis and the radius vector OP be θ, this angle being measured from the north pole to the south, so that in the figure NOP = θ.
We will now put this expression into another and more useful form, to which it is for our purposes practically equivalent. Let O, the middle point of the line NS, be the centre of the magnet; let OP=r, ON = OS = l, so that 2l is the length of the magnet, and let the angle between the magnetic axis and the radius vector OP be θ, this angle being measured from the north pole to the south, so that in the figure NOP = θ.