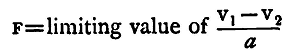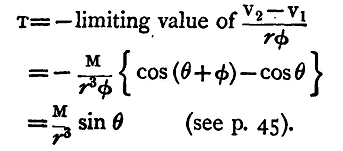Force due to a Solenoidal Magnet

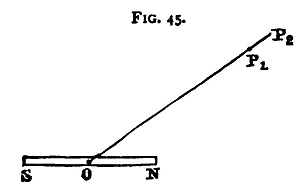
To obtain this we must remember that the work done on a unit pole by the forces of any system in going from a point P₁ to a second point P₂, V₁, V₂ being the potentials at P₁ and P₂, is V₁ - V₂. Let a be the distance between these two points, and let F be the average value of the magnetic force acting from P₁ to P₂ resolved along the line P₁P₂. Then the work done by the force F in moving the pole is Fa.

Hence

Fa = V₁ - V₂

and if the distance a be sufficiently small, F, the average value of the force between P₁ and P₂ may be taken as the force in the direction P₁P₂ at either P₁ or P₂.

when a is very small

Let us suppose that P₁, P₂ are two points on the same radius from O, that OP₁=r and OP₂=r+δ.

Then θ is the same for the two points, and we have

neglecting (δ/r)² and higher powers (see p. 42).

Also, in this case, a=δ. Thus

We shall denote this by R, so that R is the force outwards, in the direction of the radius-vector, on a unit pole at a distance r from the centre of a small solenoidal magnet of moment M. If the radius-vector make an angle θ with the axis of the magnet, we have

Again, let us suppose that P₁P₂ (fig, 46) is a small arc of a circle with O as centre, so that

OP₁=OP₂=r
let P₁ON = θ
and P₂ON = θ+φ.

Thus

a=P₁P₂ = OP₁ x P₁OP₂ = rφ.

The force, in this case, will be that at right angles to the radius vector, tending to increase θ; if we call it T we have

These two expressions are approximately true if the magnet NS be very small and solenoidal. We may dispense with the latter condition if the magnet be sufficiently small; for, as we have said, any carefully and regularly magnetised bar behaves approximately like a solenoid with its poles not quite coincident with its ends. In such a case 2l will be the distance between the poles, not the real length of the magnet, and 2ml will still be the magnetic moment.