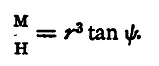Measurement of Magnetic Force

The theoretical magnets we have been considering are all supposed to be, in strictness, simply solenoidal rods without thickness, mere mathematical lines in fact.

The formulae may be applied as a first approximation, however, to actual magnets, and we shall use them in the experiments to be described.

There remains, however, for consideration the theory of an experiment which will enable us to compare the magnetic moments of a magnet of any form under different conditions of magnetisation, or of two magnets of known form, or to compare the strengths of two approximately uniform magnetic fields, or, finally, in conjunction with the formulae already obtained, to measure the moment of the magnet and the strength of the field in which it is.

We have seen (p. 144) that, if a body, whose moment of inertia about a given axis is K, be capable of vibrating about that axis, and if the force which acts on the body after it has been turned through an angle θ from its position of equilibrium, tending to bring it back to that position, be μθ, then the body will oscillate isochronously about this position; also if the time of a complete small oscillation be T, then T is given by the formula

We shall apply this formula to the case of a magnet. We have seen already that, if a magnet be free to oscillate about a vertical axis through its centre of gravity, it will take up a position of equilibrium with its magnetic axis in the magnetic meridian. The force which keeps it in the meridian arises from the horizontal component of the earth's magnetic force; and if the magnet be disturbed from this position through an angle θ, the moment of the couple tending to bring it back is MHsinθ, M being the magnetic moment. Moreover, if θ be the circular measure of a small angle, we know that the difference between θ and sinθ depends on θ³ and may safely be neglected; we may put, therefore, with very high accuracy, if the magnet be made to oscillate only through a small angle, the value θ for sinθ in the above expression for the moment of the couple acting on the magnet, which thus becomes MHθ; so that, if K be the moment of inertia of the magnet about the vertical axis, the time of a small oscillation T is given by the equation

T can be observed experimentally, and hence we get an equation to find MH, viz.

If we have in addition a relation which gives the ratio of M/H from the two we can find M and H. Such a relation has been obtained above (p. 364), and with the notation there employed we have

We shall discuss the experimental details shortly.