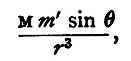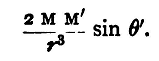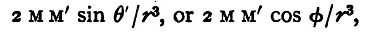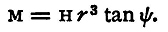Effect on a Second Magnet

In practice we require to find the effect on two magnetic poles of equal but opposite strengths, not on a single pole, for every magnet has two poles.

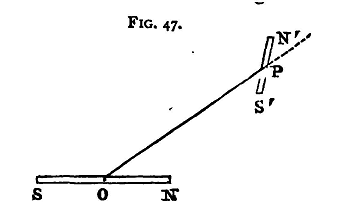
Let us suppose that P (fig. 47) is the centre of a second magnet N'PS' so small that we may, when considering the action of the distant magnet NOS, treat it as if either pole were coincident with P, that m' is the strength, and 2l' the length of this magnet, and θ' the angle between PN' and OP produced.

Then we have, acting outwards parallel to the radius vector OP on the pole N', a force

and an equal and parallel force acting inwards towards O on the pole S'; these two constitute a couple, the arm of which will be 2l'sinθ'. Thus, if M' be the magnetic moment of the second magnet, so that M' = 2m'l', we have acting on this magnet a couple, tending to decrease θ', whose moment will be

This arises from the action of the radial force R. The tangential force on N' will be

tending to increase θ' and on S' an equal force also tending to increase it. These constitute another couple tending to increase θ'; the arm of this couple will be 2l'cosθ, and its moment will be

Thus, combining the two, we shall have a couple, the moment of which, tending to increase θ', will be

It must of course be remembered that these expressions are only approximate; we have neglected terms which, if the magnets are of considerable size, may become important.

Two cases are of considerable interest and importance. In the first the axis of the first magnet passes through the centre of the second. The magnet NS is said to be 'end on.' In this case (fig. 48) we have θ=0, and the action is a couple tending to decrease θ', the moment of which is

If no other forces act on the second magnet, it will set itself with its axis in the prolongation of that of the first magnet.

In the second case (fig. 49) the line joining the centres of the two is at right angles to the axis of the first magnet, which is said to be 'broadside on'; then θ = 90°, and we have a couple tending to increase θ', the moment of which will be

We may notice that for a given value of r, the maximum value of the couple in this second case is only half of its maximum value in the former case.

The position of equilibrium will be that in which cosθ = 0, or when the two axes are parallel. Let us suppose that the second magnet is capable of rotating about a vertical axis through its centre, in the same way as a compass needle; it will, if undisturbed, point north and south under the horizontal component of the magnetic force due to the earth; let us call this H. Place the first magnet with its north pole pointing towards the second, and its centre exactly to the west of that of the second. The second will be deflected, its north pole turning to the east. Let θ be the angle through which it turns, then clearly θ' = 90-φ. The moment of the earth's force on the magnet is M'Hsinφ, that of the couple due to the other magnet is

in the opposite direction. But the magnet is in equilibrium under these two couples, and hence we have

Thus

Next place the first magnet with its north pole west and its centre exactly to the south of the second; the north pole of the second will move to the east through an angle ψ, say, and in this case we shall have θ' = ψ.

The moment of the couple due to the earth will be as before M'Hsinψ; that due to the first magnet is

and hence

We shall see shortly how these formulae may be used to measure M and H.