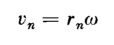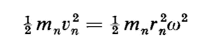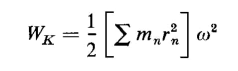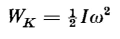Energy Stored in a Rotating Flywheel

There are many applications in which a flywheel is used alternately to store and give up kinetic energy. Examples are reciprocating engines, compressors in which there are power pulsations, and punch presses where the power is expended in a relatively short part of the duty cycle.

A body in pure translational motion has a kinetic energy of mv²/2 because all parts of the body have the same velocity. However, in the case of a rotating body all parts do not have the same velocity. Parts near the axis of rotation have relatively low velocities and those further removed from the axis have greater velocities in direct proportion to their distances from the center of rotation. All parts, however, have the same angular velocity. Hence, the velocity of a particle of mass m_n located at a distance r_n from the axis of rotation would have a tangential velocity of

where ω is the angular velocity in radians per sec.

The kinetic energy of rotation for such a particle is expressed by

Hence, for the entire rotating body

The quantity Σm_nr_n² is known as the moment of inertia and is represented by the symbol I, hence

[1-85]

If I is expressed in kilogram meters² and ω in radians per sec, then the kinetic energy is expressed in joules.

As an example, the moment of inertia of a solid cylinder rotating about its central axis is I = mR²/2 where R is the radius of the cylinder. The moment of inertia, I = (R₁² + R₂²)/2 is that of another common shape namely an annular cylinder with inside and outside radii of R₁ and R₂ respectively.