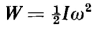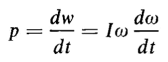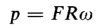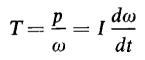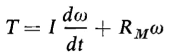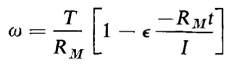Power and Torque

The work done in accelerating a rotating body from rest to an angular velocity of ω radians per sec is equal to the kinetic energy of rotation, hence, from Eq. 1-85

[1-86]

However, power is the rate of doing work, and we have

[1-87]

where dω/dt is angular acceleration in radians per sec².

Suppose that, to develop the power expressed by Eq. 1-87, an external force F is applied to a point at a distance R from the center; then from p = Fv it follows that

[1-88]

because v = Rω.

The product FR is called torque and in the rationalized MKS system is expressed in newton meters. Thus, if the torque is expressed by T = FR, Eq. 1-88 becomes p = ωT, and we have

[1-89]

the torque required to accelerate a rotating mass. This also expresses the torque developed by a decelerating mass.

Suppose that a constant torque T is applied to a flywheel starting from rest and that the moment of resistance of the bearings and other moving parts can be represented by R_M. Then if the moment of inertia of the flywheel is I, we have

[1-90]

the solution of which is

[1-91]

Note that this expression for angular velocity has the same form as that for a current in an inductive circuit with constant applied d-c voltage, as in Eq. 1-40. The moment of resistance R_M corresponds to the electrical resistance of the circuit, and the moment of inertia I corresponds to the self-inductance L. Furthermore, the energy stored in the flywheel is expressed by Iω²/2, and the energy stored in the self-inductance is expressed by Li²/2.