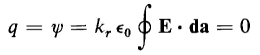Charge Within a Conductor That has a Static Charge

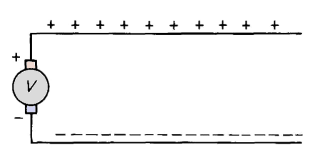
Consider two wires insulated from each other. One is connected to the positive side of the d-c source, and the other to the negative side of the d-c source as shown in Fig. 2-8.

Figure 2-8. Linear conductors connected to a d-c source

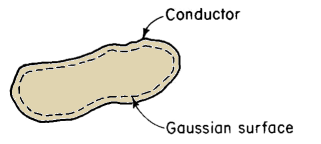
The upper wire receives a positive charge, and the lower wire a negative charge. These charges are static, i.e., they are not in motion once they are established, and there is no difference of potential from one end of a wire to the other. In other words the electric field intensity E within the wires is zero. If the wires were # 18 AWG copper, a size commonly used in lamp cord, a field intensity E along the wires of only one v per m would produce a current of about 50 amp. Therefore, when there is no current within a conductor the electric field intensity E everywhere within a conductor is zero. Accordingly, it can be shown by means of Gauss's theorem that the static charge is on the surface of a conductor. Figure 2-9 shows a conductor that carries a static charge. The broken line represents a Gaussian surface an infinitesimal distance inside the actual conductor surface. Since the charge

Figure 2-9. A Gaussian surface just in-side the surface of a conductor with a static charge

on the conductor is static, there is no flow of current within the conductor. The electric field intensity E must therefore be zero within the Gaussian surface. Hence from Eq. 2-20

[2-22]

This means that there is no charge within the Gaussian surface and the entire static charge must be on the surface of the conductor. This is true also for a hollow conductor. Therefore a charge outside of the conductor does not produce an electric field inside the hollow. However, a charge inside the hollow will produce an electric field that follows from Gauss's theorem outside the conductor.