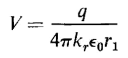Uniformly Distributed Charge on an Isolated Sphere

The derivations of flux density and electric field intensity in this chapter so far have centered around an electrical charge concentrated at a point. And although the concept of the point charge is useful for analytical purposes, it is an unrealistic one because in actual physical arrangements charges are distributed within finite volumes over surfaces that are finite. Equation 2-13 shows that the potential of a finite electric charge concentrated to a point would be infinite because r would need to approach zero to satisfy the mathematical concept of a point.

The sphere is one of the simplest configurations on the surface of which an electric charge might be distributed. Consider a conducting sphere, isolated in free space, with a charge of q coulombs uniformly distributed over its surface. If the radius of the sphere is r₁ m as indicated in Fig. 2-10 then the density of charge on the sphere's surface is

[2-23]

Figure 2-10. Conducting sphere with uniformly distributed charge

The right-hand side of Eq. 2-23 is the same as the right-hand side of Eq. 2-4. This shows that the electric field intensity at a point an infinitesimal distance external to the surface of the sphere is exactly the same as it would be if the sphere were removed and the charge formerly on the sphere's surface were concentrated at the point formerly occupied by the center of the sphere.

From this it follows that the field external to the sphere due to a uniformly distributed charge on the surface is the same as that for a charge concentrated at the center of the sphere. Thus in Fig. 2-10 the electric flux density at a distance r from the center is expressed by Eq. 2-4.

The potential of the sphere with respect to an infinitely remote point must be the same as that of the point at an infinitesimal distance from the surface as expressed by Eq. 2-13, i.e.

If the sphere were isolated in a medium of infinite extent and had a relative dielectric constant k_r, the voltage of the sphere would be

[2-24]