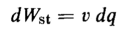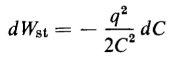Mechanical Energy and Force in a Capacitor

Figure 2-26. Movable plate capacitor

Figure 2-26 shows a simple two-plate capacitor, the plates of which are in a liquid or gaseous medium and are free to move with respect to each other. If a voltage v is applied to the plates of the capacitor a positive charge is distributed on one plate and an equal charge of opposite polarity is distributed on the other plate. These charges produce a force of attraction between the plates, and if the left-hand plate is fixed while the right-hand plate is free to move, a force f is developed and tends to move the right-hand plate toward the left. As a result electrical energy is converted to mechanical energy. However, the conversion of electrical energy to mechanical energy is generally accompanied by a change in the amount of energy stored in the dielectric. If the dielectric is lossless then all the energy absorbed by the dielectric is stored in reversible form and we have

[2-83]

where

dW_e = differential energy supplied by the electrical source in time dt
dW_st = differential energy stored in the dielectric in time dt
dW_mech = differential mechanical energy output of the capacitor in time dt

[2-84]

but

[2-85]

Substitution of Eq. 2-85 in 2-84 gives

[2-86]

It must be remembered that Eq. 2-86 is valid only for a fixed configuration of dielectric. The energy absorbed by the dielectric in changing the charge from q₁ to q₂ is

[2-87]

If the initial charge in the capacitor is zero, then the energy absorbed by the dielectric when the charge q is established is

[2-88]

In these equations the charge q is a function of the voltage across the capacitor expressed by Eq. 2-25 as q = vc.

If the dielectric constant has a fixed value, then for a given configuration of the dielectric the capacitance C in Eq. 2-25 is constant, and the result of carrying out the integration in Eq. 2-88 is

[2-89]

Equation 2-89 expresses the energy that is stored in the dielectric of a lossless capacitor of capacitance C farads. This is true whether C is constant or variable. W_st is the stored energy for the particular value of C at a given instant regardless of what the value of C was prior to that instant or the value it might attain at some later instant. From Eq. 2-89 it is evident that a change in the applied voltage v or a change in the capacitance C produces a change in the stored energy. Hence, in general, the differential energy stored in the dielectric in time dt is expressed by

[2-90]

The differential energy supplied by the source is expressed by Eq. 2-86 whether the capacitance is fixed or variable, and if Eq. 2-25, 2-86, and 2-90 are substituted in Eq. 2-83 the result is

[2-91]

and the differential mechanical energy is

[2-92]

Equations 2-90 and 2-92 show that for a constant applied voltage (dv = 0) the differential mechanical energy equals the differential stored energy. Substitution of Eq. 2-25 in 2-92 yields

[2-93]

When Eq. 2-25 is substituted in Eq. 2-90 the result is

[2-94]

If q is held constant (this can be done by disconnecting the capacitor from the electrical source) the differential stored energy is expressed by

[2-95]

This is to be expected because there is no differential electrical energy input, and the differential mechanical energy must therefore result from a change in the stored energy.

Equations 2-92 and 2-93 show that motor action results from an increase in the capacitance, which also follows from the fact that the coulomb forces act in such a direction as to increase the capacitance. The forces that are developed by an electric field in a dielectric are always in a direction that produces a dielectric configuration such that the capacitance becomes a maximum.

The mechanical power developed during the differential time according to Eqs. 2-92 and 2-93 is

The force on the plates of the capacitor is found from

to be

[2-96]

If the arrangement is such that the developed forces produce rotation, the torque is expressed by

[2-97]

A practical application of converting the energy stored in a dielectric to electrical energy by means of mechanical energy input is in the use of the capacitor microphone, also known as the condenser or electrostatic microphone. In this application, sound waves cause motion of a diaphragm that is one plate of an electrically energized capacitor in which the other plate is fixed.