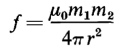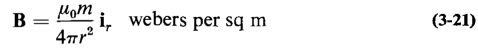The Unit Magnet Pole

It is shown in Chapter 2 that electric charges produce an electric field and that forces between electric charges exist. The force between point charges isolated in free space is given by Eq. 2-1, which expresses Coulomb's law for point electrical charges. A similar law known as Coulomb's law of force between point magnetic poles applies to magnetic fields in free space and is given by the following formula

[3-19]

where m₁ and m₂ are the strengths of two magnetic poles in terms of unit magnet poles. If the poles are of like polarity the force is one of repulsion and if the poles are of opposite polarity they are attracted toward each other. A unit magnet pole is defined as one that exerts a force of one dyne (10^-7 newton) on another unit magnet pole when poles are in free space and separated from each other by a distance of one cm. In the rationalized MKS system the force F is expressed in newtons and the distance r in meters. The term μ₀ expresses the magnetic permeability of free space having a value of 4π x 10^-7 h per m.

Figure 3-6. Lines of force of a bar magnet

The concept of a magnet pole arises from the observation that the flux from a bar magnet emanates into surrounding space from a region within the magnet near one end and enters a region within the magnet located similarly with respect to the other end as shown in Fig. 3-6. Such observations are based on the pattern assumed by iron filings when placed in the space surrounding the magnet and on experiments in which the field is explored with a magnetic compass.

According to convention, the magnetic flux leaves the north (north-seeking) pole and enters the south pole, the lines of flux continuing on through the body of the magnet and closing upon themselves. Actually a north pole cannot be isolated from its companion south pole and vice versa. However, one can conceive of a slender magnet of such great length that when one of the two poles placed at a point in the magnetic field from some other source such as another bar magnet or an electric circuit, the other pole is so far removed from the point in the field that the force on it is negligible.

Permanent magnets produce a magnetic field even when there is no excitation by means of an electric current external to the magnets. In such magnets the flux is produced by currents within the magnets that result from uncompensated electron spins, a feature of ferromagnetic materials such as iron and cobalt.

The magnetic flux that emanates from a magnetic pole having a strength of m units is expressed by

[3-20]

An imaginary magnetic pole of such strength concentrated to a point and isolated in free space would produce a magnetic flux density at a distance of r m of

[3-21]

A comparison of Eq. 3-21 with Eq. 3-15 shows that the magnetic field intensity in terms of unit poles is expressed by

[3-22]

The force developed between unit magnetic poles for a given separation is very feeble in comparison with that developed between equal charges of one coulomb at the same separation. From Eq. 2-1 the force developed between two charges of one coulomb each is

and that developed between two unit magnetic poles at the same separation, according to Eq. 3-19, is expressed by

Division of Eq. 3-23 by Eq. 3-24 yields

where c = 2.998 x 10⁸ m per sec, which is the velocity of light or the velocity of an electromagnetic propagation in free space.

The concept of the unit magnet pole is useful for analytical exploration of the magnetic field since it brings out in a quantitative manner the fact that the magnetic field is a field of force and is comparable in some respects, although not entirely, to the electric field. Some of the relationships derived for the magnetic field, shown with their counterparts relating to the electric field, are shown in Table 3-1.

Table 3-1. Magnetic Quantities In Terms Of The Unit Pole And Electric Quantities In Terms Of Electric Charge
	Magnetic		Electric
Quantity	Formula	Unit	Formula	Unit
Field Intensity	H = m/(4r2π)	amperes/meter	E = q/(4r2πε0)	volts/meter
Flux Density	B = μ0m/(4r2π)	webers/square meter	D = q/(4r2π)	coulombs/square meter
Flux	φ = μ0m	webers	ψ = q	coulombs