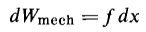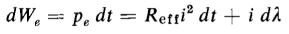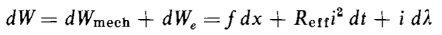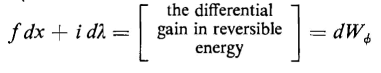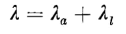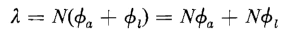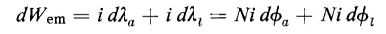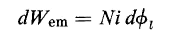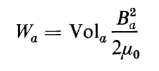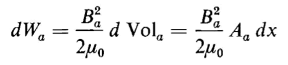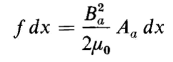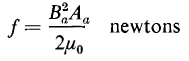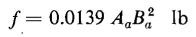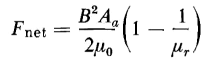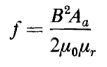Magnetic Force in Terms of Flux Density

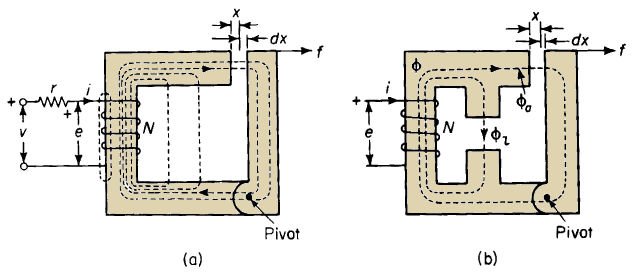
The magnetic flux that crosses the air gap in a structure of magnetic material produces a force of attraction between the faces of the air gap. This force, which can be exerted only on materials with a relative permeability μ_r greater than unity, is a function of the magnetic flux density B_a in the air gap as shown in the following derivation.

Figure 3-25. Electromagnet (a) approximate flux path; (b) simplified flux path.

A simple iron structure with an air gap of length x, and with plane parallel faces is shown in Fig. 3-25(a). Fringing at the air gap can be neglected for short air gaps. A pivot, shown in the bottom of the structure, makes it possible to vary the length of the air gap.

Assume a current of i amp, in the N turns of the exciting winding, producing a magnetic flux distributed approximately as shown in Fig. 3-25(a). Part of this flux crosses the air gap, the remainder is leakage flux. A further simplification of the flux paths is indicated in Fig. 3-25(b) where

Φ_a is the flux that crosses the air gap,
Φ_l is the equivalent leakage flux, and
Φ = Φ_a + Φ_l is the equivalent flux linking all N turns of the winding.

Now if a force f is applied to the movable member of the structure causing the air gap to increase its length by an amount equal to the differential distance dx, a differential amount of mechanical energy is put into the field. The differential amount of energy may also be accompanied by a positive or negative contribution of energy to the field from the electrical source. The energy input to the field corresponds to "the gain in reversible energy" in Eq. 1-3, which for the case under discussion can also be written as

[3-66]

The work done by the force f in increasing the air gap by the differential distance dx is the mechanical differential energy input

[3-67]

whereas the electrical differential energy input is

[3-68]

where

dt = the differential time in which the displacement dx occurs
R_eff = the effective resistance that includes the ohmic resistance of the winding and takes into account the energy dissipated in the form of heat due to hysteresis and eddy currents in the iron resulting from time variations in the flux
λ = flux linkage with the TV-turn winding

The total differential energy input to the electromagnet in Fig. 3-25 is the sum of the mechanical and electrical input, or

[3-69]

The quantity R_effi² dt represents the electrical energy converted into heat and accounts for two terms in Eq. 1-3 as follows

In this case the energy that leaves the magnet is in the form of heat transmitted to the surrounding medium, and the gain in irreversible energy is that evidenced by the increase in the temperature of the various parts of the electromagnet. These components of differential energy make no contribution to the energy stored in the magnetic field.

To account for the term remaining in Eq. 1-3 the following must hold

and in which the reversible energy is the energy stored in the magnetic field. The quantity i dλ is the electromagnetic differential energy dW_em supplied by the source of voltage and is necessary to produce any change in flux linkage. The flux linkage can be divided into two components on the basis of Fig. 3-25(b). These are

where

with Φ_a being the flux that crosses the air gap and Φ_l the equivalent flux in the leakage path.

Suppose that the current i in the winding is adjusted so that the flux Φ_a in the air gap remains constant while the displacement dx transpires. Then dΦ_a is zero and the electromagnetic differential energy supplied by the source is

which means that the only contribution made by the voltage source to the reversible energy is that stored in the leakage field only. The voltage source makes no contribution whatsoever to the reversible energy in the air gap. It follows, therefore, that as long as the flux in the air gap remains constant, any gain in the energy stored in the field of the air gap must equal the mechanical energy input f dx.

The permeability μ₀ of the air gap is independent of B, i.e., is constant, and Eq. 3-62 therefore applies to the energy stored in the air gap since the faces of the gap are parallel planes making the flux density B_a uniform throughout since fringing is neglected. Hence

and if the flux density B_a is constant, the differential air gap energy is

[3-70]

the volume of the air gap being Vol_a = A_ax.

Equation 3-70 must also represent the mechanical input as long as B_a is constant. This leads to the relationship expressed by

and the force is therefore

[3-71]

where

B_a is in webers per square meter,
A_a is in square meters, and
μ₀ = 4π x 10^-7 h per m.

When the flux density is expressed in kilolines per square inch and the area of the air gap in square inches, the force, expressed in pounds, is

[3-72]

It should be remembered that no magnetic force is exerted on a material that has a relative permeability μ_r of unity. If the toroid of Fig. 3-9 had a wooden core interrupted by an air gap at right angles to the flux path there would be no force on the faces of that gap regardless of the current in the winding, whereas an iron core would experience a force in accordance with Eqs. 3-71 and 3-72. In any electromagnet the force on the steel or magnetic faces of the air gap or pole pieces is only that due to the flux that exists over and above the flux that would exist if the pole pieces were replaced by air. Therefore the actual force on the faces of the air gap is proportional to the difference between the effect of iron and the air, so that

[3-73]

The correction term 1/μ_r is generally negligible, but it may be appreciable in the case of high saturations or slightly magnetic materials.

If the air gap were replaced by a magnetic material having a constant relative permeability of μ_r the amount of energy stored in that material for a given value of B_a would be 1/μ_r, that of the air gap. The force therefore would be reduced in the same proportion and Eq. 3-71 would be modified to

[3-74]