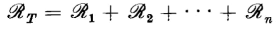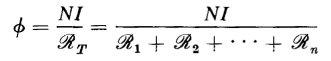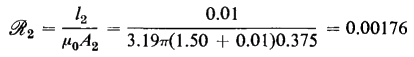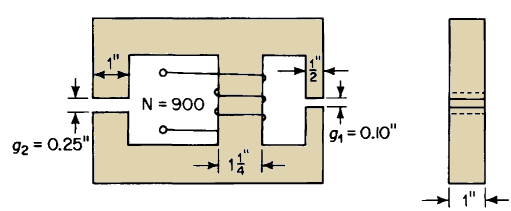
Magnetic Circuits in Series and in Parallel

Although the magnetic circuit is similar in many aspects to the electric circuit, calculations of magnetic circuits are generally more complex because of magnetic leakage and because of the nonlinearity of magnetic materials. Equation 3-43 expresses the relation between the magnetic flux and the mmf in a magnetic circuit of uniform cross section A and length l. In that equation the quantity μA/l is known as the permeance P, which is the reciprocal of the reluctance R. If we had a single magnetic circuit with n components in series for which the reluctances would be

we could get the total reluctance simply as follows, provided that there is no leakage

[3-113]

If the total mmf is Nl then the flux in such a circuit is found to be

[3-114]

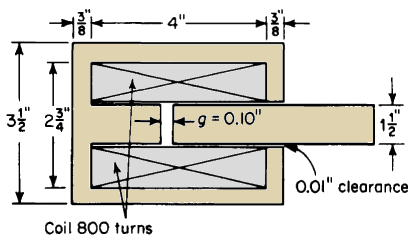
However, since the values of the various permeabilities μ₁, μ₂.....,μ_n depend upon the degree of magnetization, which is generally different for a given value of Φ since the n components that the relationship suggested in Eqs. 3-113 and 3-114 are not particularly useful. It is, therefore, generally more convenient to compute the mmfs for each component for a given value of flux Φ on the basis of the magnetization curve for that component.

However, in the cases of magnetic circuits that have air gaps in series and in which the iron is unsaturated so that its reluctance is small in comparison with that of the air gaps, useful approximations can be made by computing the reluctance of each of the air gaps and taking their sum as the total reluctance.

Example 3-6:

An electromagnet with a cylindrical plunger is shown in Fig. 3-42. Neglect the reluctance of the iron, leakage, and fringing and determine the flux in the magnet when the 800-turn coil carries a current of 3.5 amp.

Solution:

There are two air gaps in series, namely the 0.10-inch gap within the coil and the concentric air gap 0.01 in. in length between the throat and the plunger. Since all dimensions are given in inches the mixed English system of units will be used for the calculations. Figure 3-42. Plunger-type electromagnet The magnetic reluctance of 0.10-in. air gap is and that of the 0.01-in. air gap between the plunger and throat of the magnet is The total reluctance is the sum of the two reluctances and ...

The reasoning that applies to the series magnetic circuit also holds for the parallel magnetic circuit and for rigorous calculations the fluxes in the various parallel branches are computed for a given value of mmf using the magnetization curves. Again if the iron is unsaturated and there are air gaps in parallel of such lengths that the reluctance of the iron is negligible the permeance, which is the reciprocal of reluctance, of the magnetic circuit is the sum of the permeances of the various air gaps provided that leakage is negligible. When the leakage is appreciable the permeance of the leakage paths must be added to those of the air gaps to obtain the total permeance.

Example 3-7:

Figure 3-43 shows an electromagnet with two air gaps in parallel. Neglect leakage and the reluctance of the iron but correct for fringing and determine the flux in each air gap and the total flux when the current in the 900-turn winding is 2.0 amp. Figure 3-43. Electromagnet with two air gaps in parallel

Solution:

Since there are two air gaps in parallel their combined permeance is the sum of their permeances. The permeance of the 0.10-in. air gap g1 is Since the reluctance of the iron is negligible and the two air gaps are in parallel the entire mmf is expended across each air gap, and the flux in the 0.10-in. air gap is The permeance of the 0.25-in. air gap g2 is and the flux in the 0.25-in. air gap is The total flux, which is the flux in the middle leg, is The total flux can also be found from the total permeance and the mmf as follows