| 5-1 |
A 400-cycle emf of 100 v is applied to the winding of the electromagnet in Fig. 3-17. Assume a stacking factor 0.95 for the laminated core and neglect the resistance of the winding.
(a) Determine the maximum flux density Bm in the core if the wave form of the voltage is sinusoidal.
(b) Neglect the effect of air gaps in the core and determine the max value of the exciting current if the core is composed of U.S.S. Annealed Electrical Sheet Steel (see Fig. 3-11).
(c) Repeat parts (a) and (b) for a 400-cycle emf of 130 v.
(d) Repeat parts (a) and (b) for a core thickness of 1.25 in. instead of 1.50 in.
(e) Repeat parts (a) and (b) for a core thickness of 1.75 in. instead of 1.50 in.
(f) Using the dimensions of the core as shown in Fig. 3-17 determine the 400-cycle voltage that will give twice the max value of current as in part (b).
(g) Using the dimensions of the core shown in Fig. 3-17, determine the frequency that will give twice the max value in part (a) at 100 v.
|
| 5-2 |
A reactor has a laminated core of U.S.S. Annealed Electrical Sheet Steel of the dimensions shown in Fig. 3-17. Assume a stacking factor of 0.95 for the core and neglect the resistance of the winding.
(a) Determine the number of turns in the exciting winding such that the max flux density Bm is 90,000 lines per sq in. for a 60-cycle emf of 240 v.
(b) Neglect air gaps in the core and determine the max value of the current for the condition of part (a) above,
(c) If the winding in parts (a) and (b) is composed of two identical parts, i.e., equal number of turns and equal amounts of copper, what value of 60-cycle voltage should be applied to the two halves of the winding connected in parallel such that the max flux density Bm is 90,000 lines?
(d) What is the max value of the current supplied by the source for the condition of part (c) above?
(e) What is the max value of the current in each half of the winding for the condition of part (c) above?
|
| 5-3 |
Repeat Problem 5-1 (a) and (b) if the voltage is a square wave.
|
| 5-4 |
A certain reactor has a core of net cross section A0. The length of the flux path in the core is l0. The exciting winding has N0 turns and is rated at V0 v at a frequency of f0 cps. The peak value of the current is Im0. The core losses are Pc0 and the flux density is Bm0.
Another reactor of the same construction, except that all its linear dimensions are 1.5 times those of the reactor in Problem 5-4, operates at the same value of flux density Bm0 and at the same voltage V0 and the same frequency f0. Determine
(a) The number of turns in the winding of the larger reactor in terms of the turns N0 of the first reactor.
(b) The max value of the current in the larger reactor in terms of Im0
(c) The core loss in the larger reactor in terms of Pc0.
|
| 5-5 |
A sinusoidal voltage impressed on one winding of a transformer has a value such that the maximum flux density Bm in the core is 10,000 gausses. Data for the upper half of the hysteresis loop for a maximum flux density of 10,000 gausses are tabulated below.
B
[Gausses] |
H
[Oerstedts] |
B
[Gausses] |
H
[Oerstedts] |
| 0 |
0.55 |
9000 |
1.17 |
| 2000 |
0.65 |
8500 |
0.83 |
| 4000 |
0.78 |
8000 |
0.57 |
| 6000 |
1.03 |
7000 |
0.18 |
| 7000 |
1.23 |
6000 |
-0.07 |
| 8000 |
1.50 |
4000 |
-0.33 |
| 9000 |
1.89 |
2000 |
-0.46 |
| 10000 |
2.39 |
0 |
-0.55 |
| 9500 |
1.67 |
|
|
Plot the complete hysteresis loop and the wave form of the exciting current as shown in Fig. 5-3, neglecting the effect of eddy current and the effects of joints in the magnetic circuit.
NOTE: Joints increase the magnetic reluctance of the core because in those regions the flux enters small air gaps.
|
| 5-6 |
Repeat Problem 5-5, but for sinusoidal exciting current.
|
| 5-7 |
A reactor with a winding of negligible resistance has an exciting current that is expressed approximately by
iexc=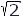 [10.4 cos (377t - 79°) + 4.5cos(1.131t + 90°) + 1.1cos(1.885t - 90°)] [10.4 cos (377t - 79°) + 4.5cos(1.131t + 90°) + 1.1cos(1.885t - 90°)]
when the applied voltage is
v = 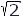 [l20cos 377t] [l20cos 377t]
Determine
(a) The real power in watts.
(b) The effective value of the exciting current.
|
| 5-8 |
Plot waves of the voltage and the fundamental, 3rd harmonic, and 5th harmonic components of the exciting current along with the total exciting current in Problem 5-7.
|
| 5-9 |
Using the data of Problem 5-7
(a) Determine
(i) The effective value of the core-loss current.
(ii) The effective value of the fundamental component in the magnetizing
current, (iii) The effective value of the total magnetizing current.
(b) Draw to scale a phasor diagram, as shown in Fig. 5-9, showing the voltage, exciting current, core-loss current, fundamental component of magnetizing current, the total magnetizing current, and the phase angle
Φexc
(c) Write the equation for the instantaneous magnetizing current.
|
| 5-10 |
A Transformer with 450 primary turns, when energized from a 120-v, 60-cycle line, draws a no-load current of 1.5 amp. The no-load power is 82 w. Neglect the resistance of the winding and leakage flux and determine
(a) The core-loss current.
(b) The magnetizing current.
(c) The maximum flux in the core.
(d) The exciting admittance Y.
(e) The exciting conductance G.
(f) The exciting susceptance B.
|
| 5-11 |
Draw an equivalent series circuit for the transformer of Problem 5-10 based on the circuit of Fig. 5-10(c). Evaluate rc and x.
|
| 5-12 |
The primary winding of the transformer in Problem 5-10 has a resistance of 0.035 ohm.
(a) Find the value of the induced emf E.
(b) Show the equivalent circuit of the transformer and its primary, based on Fig. 5-10(b), indicating the numerical values of all the quantities shown in Fig. 5-10(b).
(c) Repeat part (b) above, but for Fig. 5-10(c).
|
| 5-13 |
How are the magnitudes of the quantities in parts (b) and (c) of Problem 5-12 affected by an increase in the frequency if the voltage is held constant ?
|
| 5-14 |
Determine the volume of air gap in a 60-cycle, 75-v, 20-amp reactor that is designed to operate at a maximum flux density 85 kilolines per sq in. Neglect the reluctance of the iron, fringing and leakage.
|
| 5-15 |
The reactor of Problem 5-14 has 130 turns. Determine
(a) The length of air gap.
(b) The cross-sectional area of the core.
|
| 5-16 |
Neglect iron losses and determine
(a) The current rating.
(b) The voltage rating of the reactor in Problem 5-14 for operation at 400 cps at Bm = 85 kilolines per sq in.
|
| 5-17 |
The magnetic flux density in the reactor of Problem 5-7 is 80,000 lines per sq in. and the winding has 40 turns. An air gap of 0.040 in. is put into the iron. Determine
(a) The effective value of the component of magnetizing current produced by the air gap.
(b) The effective value of the total magnetizing current.
(c) The effective value of the exciting current.
(d) The real power expressed in watts.
(e) The reactive power in vars.
|
| 5-18 |
A choke that carries a direct-current component of 0.50 amp has a core comprised of E and I laminations assembled to form three butt joints as
 |
| Figure 5-17. Laminations in reactor core for Problem 5-18 |
shown in Fig. 5-17. The winding consists of 1,100 turns of No. 25 AWG enamel wire. The core is stacked to a depth of 3.60 in. with a stacking factor of 0.94. The magnetic characteristics of the core material, i.e., U.S.S. Annealed Electrical Sheet Steel is shown graphically in Fig. 3-11. Estimate the smallest size of nonmetallic spacer to be placed in each of the three butt joints of the core such that saturation due to the direct current in the winding is negligible.
|
| 5-19 |
A certain 60-cycle, iron-core reactor has a hysteresis loss of 4 percent, eddy-current loss of 1 percent, and a copper (I2R) loss of 5 percent in terms of its volt-ampere rating when operating under rated conditions of current, voltage, and frequency. If this reactor is operated at a frequency of 50 cps instead of 60 cps, but at the same current density and flux density as for normal 60-cycle operation, what is
(a) The 50-cycle volt-ampere rating in terms of the 60-cycle volt-ampere rating?
(b) The percent core loss and the percent copper loss in terms of the 50-cycle volt-ampere rating?
|
| 5-20 |
A reactor has the same configuration and lamination thickness as that of Problem 5-19 with twice the volt-ampere rating at 60-cycles when operating at the same current density and flux density as that of Problem 5-19 under rated conditions. Calculate the following ratios for the larger reactor in terms of the smaller
(a) The linear dimension k.
(b) The number of turns N.
(c) The size of the conductor in the winding.
(d) The temperature rise of the winding, neglecting the change in winding resistance with copper temperature.
|


 Excitation Characteristics of Iron-Core Reactors
Excitation Characteristics of Iron-Core Reactors  Problems
Problems





 Excitation Characteristics of Iron-Core Reactors
Excitation Characteristics of Iron-Core Reactors  Problems
Problems

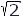 [10.4 cos (377t - 79°) + 4.5cos(1.131t + 90°) + 1.1cos(1.885t - 90°)]
[10.4 cos (377t - 79°) + 4.5cos(1.131t + 90°) + 1.1cos(1.885t - 90°)]
