3-Phase Transformers

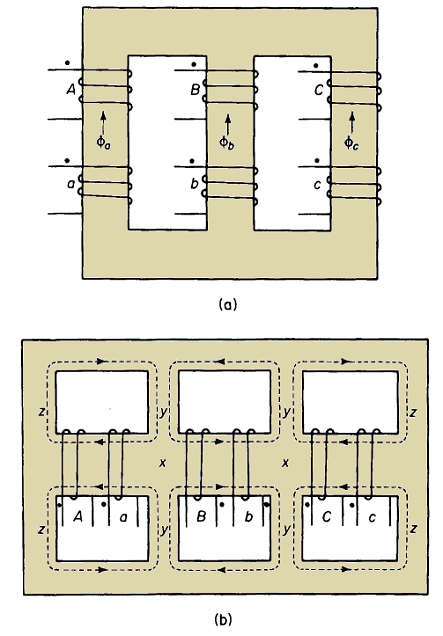
The 3-phase transformer is one that incorporates the cores and windings for all three phases in one structure, an arrangement that is generally more economical (from the standpoint of both space and costs) than a combination of three single-phase transformers of the same total rating. A 3-phase transformer is shown in Fig. 6-28. Figure 6-29 shows the schematic arrangement commonly used for the core and windings in 3-phase transformers.

Figure 6-28. 3-phase core-type transformer rated 5,000kva, 69,000/15,000 volts, 60 cycles. (Courtesy of Westinghouse Electric Corporation.)

The similarity between Fig. 6-29(a) and the construction of the core and windings in Fig. 6-28 is quite evident.

The core in Fig. 6-29(a) has only the three legs that carry the windings and does not require a fourth leg to serve as a return path for the flux because the sum of the three fluxes φ_a, φ_b, φ_c is zero for balanced 3-phase operation.

Figure 6-29. 3-phase transformers, (a) Core type; (b) shell type.

The middle windings in Fig. 6-29(b) have their polarities reversed with respect to the outer windings. Nevertheless, the polarities of the voltages across the primary and secondary windings must be consistent, relative to the polarity marks of the windings, with those shown in Figs. 6-21, 6-23, and 6-25, depending upon the kind of transformation involved - whether delta-delta, wye-wye, or wye-delta. By reversing the polarities of the middle windings, the magnetic fluxes from each adjacent phase add [in the regions x of Fig. 6-29(b)] to that of the middle phase rather than subtract from it. Subtracting from it would make for a larger core. This follows from the fact that the maximum instantaneous value of the sum of two equal magnetic fluxes 120° apart in time phase and undergoing a sinusoidal time variation equals the maximum instantaneous value of one of these fluxes, whereas the maximum instantaneous value of the difference between such fluxes equals the maximum instantaneous value of one of these fluxes multiplied by . 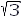Hence, if the polarities of the middle windings were the same as of the outer windings, the legs y would need to be times as wide as the legs z in Fig. 6-29(b).