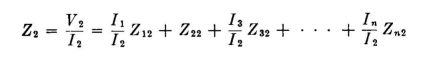Input Impedance to Each Radiator in a Directive Array

Author: Edmund A. Laport

Before one can design the feeder system for a directive array, it is necessary to predetermine the input impedance to each radiator when it is functioning properly in the final working system. Any impedance computation for this purpose therefore presupposes that the system is energized so as to provide the proper current amplitude and phase in each radiator and that the system is producing the desired pattern. From here on, the circuit-design problem is to energize each radiator as a separate load with its correct current and phase when energized from a common generator - the transmitter.

The self-impedance of each radiator at the working frequency must first be known with an accuracy of a few percent. and especially the nature of its reactive component must be certain. In preliminary computations the self-impedance may be estimated from measurements that were previously made on a similar radiator, or from measurements made on the same design of radiator, or from interpolated values from a number of sources of data that one may have from former experience. Without such previous-experience data, general data such as those from Figs. 2.15 and 2.16 may be used, with the addition of the effects of base insulators, guys and guy insulators, tower-light circuits, and other attachments that must be present in the final working system. Eventually it will be necessary to make measurements on the radiators, after they have been erected, to confirm the preliminary computations and the feeder-circuit design.

The voltage at the base (feed point) of each radiator will be

In this equation, all the currents and impedances are complex numbers, referred to some one spot in the system such as radiator 1 as a basis of reference of phases and amplitudes. This equation shows that the voltage at the base of radiator 1 is the sum of its own current times its own self-impedance, the induced voltage from radiator 2 is a result of its current times the mutual impedance between radiators 2 and 1, and the same for all the other radiators. In general, these are all complex numbers. Thus the value of V₁ will have an amplitude and also a phase relation to I₁. The ratio V₁/I₁ is the input impedance to radiator 1 and is generally complex, meaning that it has both resistance and reactance. Occasionally a radiator will have an input impedance which has a negative-resistance component. This means that this radiator is giving back power to the generator and thus acts as a second generator instead of as a load. This condition requires special precautions in the feeder-network design, because its power will be flowing in a reversed direction. It is preferable to rewrite the foregoing equation in the rectangular form that employs the inphase and quadrature current components and the resistances and reactances of the impedances. Then the equation becomes in which φn is the phase difference between the current in radiator n and that in radiator 1 which is used as the reference for all currents in the system.

This equation can be solved graphically by means of vectors or by arithmetic after inserting the correct numbers and signs for all values.

When one is merely interested in impedances, I₁ is assumed to be unity. Then all the other currents are merely expressed as ratios with respect to I₁, and the value found for V₁ is then exactly equal to the impedance of radiator 1 in resistance and reactance. The values for the mutual impedances must be carefully handled because they may lie in any of the four quadrants, and the resistive component of a mutual impedance in the second and third quadrants is therefore negative. Also, the phase of the different radiator currents may lie in any of the four quadrants.

This operation is repeated for each radiator in the system, unless symmetry of a problem makes it unnecessary for certain radiators. For example, the impedance of the second radiator will be

and so on, through all n radiators. For mutual-impedance data consult Appendix III and refs. .