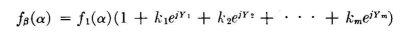Multielement Arrays of Vertical Radiators

Author: Edmund A. Laport

Not all of the problems of broadcast directive arrays can be solved with patterns of 90 or 180 degrees symmetry. In practice, asymmetrical arrays are frequently required. The computation of patterns is thus greatly complicated because direct solutions are very seldom possible. Various mechanical and electronic calculating machines have been devised to reduce the labor required to find a pattern of the desired characteristics by trial. Cumulative experience with such problems increases the facility of approach and reduces the time required to attain a solution. There are no simple rules to guide one in such cases, and usually one may not even know how many radiators are needed to obtain an acceptable asymmetrical pattern. Since there is almost no probability of any two directive broadcast situations being the same, each problem becomes a new one.

The equations for a generalized multielement array of identical vertical radiators can be expressed in several different forms, the most useful and the simplest being the vector form.

Let one radiator be the zero space-time reference, and let all other spacings, directions, phasings, and current ratios be reckoned from it. Let zero azimuth be true north, and measure azimuths ß clockwise. Reference radiator is represented by subscript 0 and other parameters associated with other radiators by subscripts 1, 2, 3, etc., to m = n - 1 for an n-radiator array.

Then, the horizontal pattern is written

in which f(β) is the relative horizontal pattern of field strength,

(may be greater or less than unity), ejXm is a unit rotating vector at an angle X with respect to reference unit vector, X_m is the phase angle of the m-th radiator field due to space and time differences with respect to reference radiator field, and X_m = S_m cos (β - β_m) + φ_m, where S_m is the electrical spacing of radiator m from radiator 0 and is always reckoned positive, βm is the azimuth of the line through radiator m and radiator 0 and ranges clockwise through 360 degrees, and φ_m is the time-phase difference between the currents I_m and I₀.

Since the geographical data which the pattern must fit are always in terms of azimuths with respect to true north, it is best to compute the pattern in the same coordinates.

The vertical pattern f β(α) through any azimuth angle β is derived from

in which f β(α) is the relative field strength at an angle above the horizon, f₁(α) is the relative vertical pattern for a single radiator, and Y_m = S_m cos[(β - βm) cos α + φ_m]. All other symbols are the same as for the preceding equations.

Once calculated, the absolute field strengths are found by making a root-mean-square measurement of the pattern, placing this root-mean-square value at the field strength corresponding to the power used and the known realizable radiation efficiency of the array, and replotting the pattern to a convenient scale of field strengths.

These general vector equations are useful for checking the patterns for an array derived by any other method.

When the radiators of a system are symmetrically disposed in a straight line, with uniform or systematic symmetrical current distributions, the trigonometric form for the radiation patterns is more convenient for computation. The final pattern can be synthesized by employing the patterns for pairs of radiators having equal fields and, if the radiators are identical, having equal currents. Certain types of problems are best solved by multiplying pair patterns and others by adding pair patterns which are cocentered. The use of these different methods will be illustrated elsewhere. Actually, radiation patterns can be expressed in a variety of ways, and the choice is finally determined by the convenience of manipulation and computation. The vector form just discussed is perfectly general and can be used without restriction of array geometry or the phases and amplitudes of the radiator currents. The vector method is convenient for graphical computations. In performing the computations arithmetically, the vector form is best converted to its real and imaginary components, adding all the real (cosine) terms, then all the imaginary (j sine) terms, and finally solving for the scalar value of the right triangle which they mutually form.

In synthesis techniques where the minimums of the pattern are being placed to achieve certain suppressions of field strength and where linear arrays with systematic current distributions can be used, the multiplication form of the pair patterns offers special advantages. However, when Fourier current gradings are employed to shape patterns in some specified manner, the trigonometric series of pair patterns is used.