 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Multivariate Data Multivariate Data  Modeling Modeling  Neural Networks Neural Networks  Training of Neural Networks Training of Neural Networks  Back Propagation of Errors Back Propagation of Errors |
|
| See also: multi-layer perceptron |   |
The basic principles of the back propagation algorithm are: (1) the error of the output signal of a neuron is used to adjust its weights such that the error decreases, and (2) the error in hidden layers is estimated proportional to the weighted sum of the (estimated) errors in the layer above.
During the training, the data is presented to the network several thousand times. For each data sample, the current output of the network is calculated and compared to the "true" target value. The error signal dj of neuron j is computed from the difference between the target and the calculated output. For hidden neurons, this difference is estimated by the weighted error signals of the layer above. The error terms are then used to adjust the weights wij of the neural network.
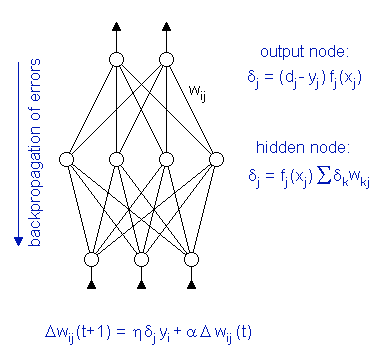
Thus, the network adjusts its weights after each data sample. This learning process is in fact a gradient descent in the error surface of the weight space - with all its drawbacks. The learning algorithm is slow and prone to getting stuck in a local minimum.
For the standard back propagation algorithm, the initial weights of the multi-layer perceptron have to be relatively small. They can, for instance, be selected randomly from a small interval around zero. During training they are slowly adapted. Starting with small weights is crucial, because large weights are rigid and cannot be changed quickly.
The following![]() shows how a multi-layer perceptron learns to model data.
shows how a multi-layer perceptron learns to model data.
Last Update: 2006-Jšn-17