You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Multivariate Data Modeling Neural Networks Models of Neural Networks RBF Neural Networks |
|
| See also: kernel estimators |   |
Radius basis function networks (RBF networks) form a special type of
neural networks, which are closely related to density estimation methods.
Some workers in the field do not regard this type as neural networks at
all. A thorough mathematical description of RBF networks is given by Broomhead
, a short introduction is also given by Lohninger . RBF networks
fall in between regression models and nearest neighbor classification schemes,
which can be looked upon as content-addressable memories. Furthermore the
behavior of a RBF network can be controlled by a single parameter which
determines if the network behaves more like a multiple linear regression
or a content-addressable memory.
RBF networks have a special architecture in that they have only three
layers (input, hidden, output) and there is only one layer where the neurons
show a nonlinear response. In addition, other authors have suggested including
some extra neurons which serve to calculate the reliability of the output
signals (extrapolation flag).
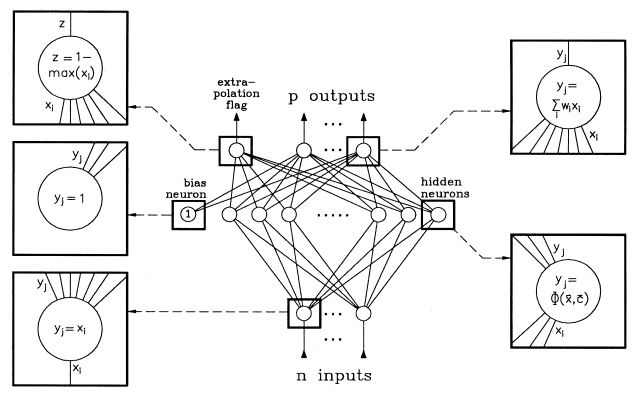
The input layer has, as in many other network models, no calculating power and serves only to distribute the input data among the hidden neurons. The hidden neurons show a non-linear transfer function which is derived from Gaussian bell curves. The output neurons in turn have a linear transfer function which makes it possible to simply calculate the optimum weights associated with these neurons.
Last Update: 2006-Jän-17