You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Bivariate Data Correlation Distribution of the Correlation Coefficient |
|
| See also: correlation coefficient, random variable, chance correlation, testing the significance of r |   |
It should be noted that the correlation coefficient r is a random variable,
thus having a distribution function which depends on the population
value of the correlation coefficient r and the
number of samples n.
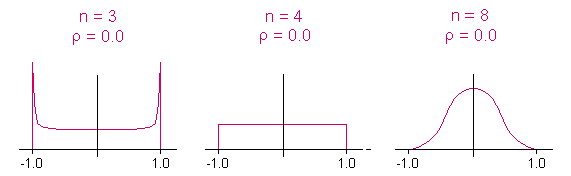
From the images above one can conclude that for a small number of observations
it is quite likely that the correlation coefficient is high. A high correlation
coefficient does not necessarily represent a high correlation between two
variables. Especially with four sample values, any correlation coefficient
is equally likely to occur. You may test this phenomenon yourself by starting
the following 
.
As a consequence of this effect, one has to test
for the significance of a correlation coefficient.
Last Update: 2005-Jul-16