You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Statistical Tests Correlation Coefficient Test: Correlation Coefficient
Index
See also: survey on statistical tests, correlation coefficient, distribution calculator, distribution of the correlation coefficient 

Test: Correlation Coefficient



A correlation coefficient of zero indicates that there is no linear relationship between two variables. In order to test the significance of a correlation coefficient we can use a test statistic t:

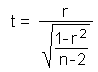
This test statistic is distributed according to a t-distribution. The correlation coefficient is considered to be statistically significant if the computed t value is greater than the critical value of a t-distribution with a level of significance of a.

In order to test the hypothesis whether a calculated correlation coefficient r is different from the population coefficient r, we have to calculate the test statistic z which exhibits a standard normal distribution. r and r are considered not to be from the same population if z is greater than the critical value of a standard normal distribution with a selected level of significance.


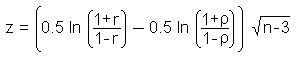
(for negative values of r, or r the absolute values have to be taken)


Last Update: 2005-Jul-16