 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
 You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information. You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Bivariate Data Bivariate Data  Time Series Time Series  Time and Frequency Time and Frequency |
|
| See also: Fourier transform, Fourier series |   |
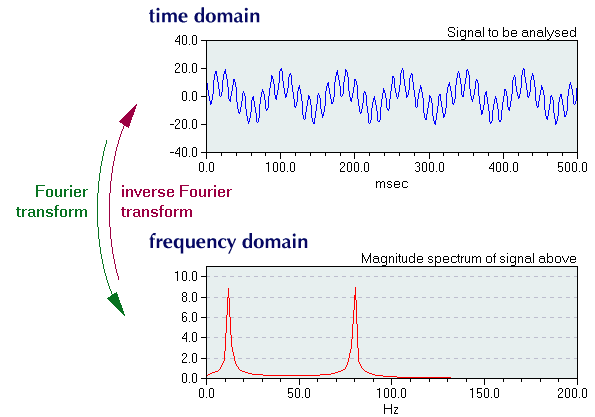
Since time and frequency are related to each other by the simple equation
time = 1 / frequency,
processing of time series may be performed by first transforming the signal from the time domain to the frequency domain, executing the intended processing, and then transforming the results back to the time domain. In many cases the operations in the time domain are easier to conduct, and sometimes easier to understand than in the time domain.
More generally speaking, we can state that, for each independent variable (i.e. the time) in the data domain (or domain of measurements), a corresponding variable with inverse dimensions (i.e. time-1 = frequency) becomes the independent variable in the spectral domain. So, abstracting from time, we can claim that any signal has a spectrum, since the spectrum is the function of the inverse variable that corresponds to the particular dependent variable in the original data:
original data: f(x)
spectrum: g(x-1)
original data and its spectrum are related by the Fourier transform (FT) and its counterpart, the inverse Fourier transform:
g(x-1) = FT [f(x)]
f(x) = FT-1[g(x-1)]
Last Update: 2006-Jšn-18