You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Math Background Matrices Singular Value Decomposition |
|
| See also: Matrix Inversion, Eigenvectors and Eigenvalues - Advanced Discussion, The NIPALS Algorithm |   |
When trying to solve linear equation systems which are singular or "near singular" by Gaussian elimination or by LU decomposition these methods fail, or result in unstable solutions. In such cases the solution can be found by a method called singular value decomposition (SVD).
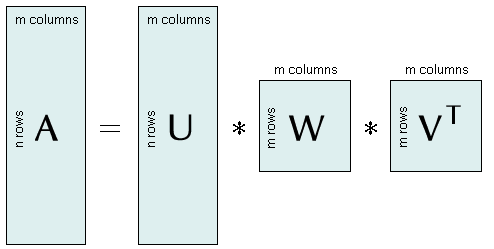
SVD is based on the theorem of linear algebra which states that a matrix A (m columns, n rows) can be transformed into a product of three matrices U, W, and VT which have specific properties: (1) the matrices U and V have orthonormal columns, (2) the matric V is quadratic, (3) the matrix W is a diagonal matrix with all non-diagonal elements equal to zero.
Last Update: 2005-Jän-25