You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
Table of Contents  Appendix Exercises Polynomial Fit by MLR |
|
| See also: MLR |   |
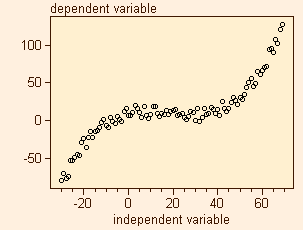Multiple
linear regression can be used to create an arbitrary polynomial fit between
two variables. The concept behind this is to calculate different powers
of the independent variable and estimate the parameters by MLR. If you
want to create a third order fit, you calculate the square and the third
power of the independent variable. In addition, you also need a variable
which is just constant, preferably 1 (to compensate for any offset in the
function to be estimated). So you end up with a matrix containing the following
variables:
You can now apply MLR to estimate the coefficients of the polynomial fit (assuming that u equals 1):
y = a + bx + cx2 + dx3
Use the data set POLYFIT and
go to the 
to create several fits of different order. Try to fit the data by a 2nd,
3rd, and 4th order polynomial. Which of the curve fittings fits best?
How can you avoid overfitting?
Hint: DataLab automatically calculates the constant
coefficient, so you don't have to provide an extra (constant) variable
for the calculations.
Last Update: 2005-Jul-16