Conditions for Oscillation

Author: Leonard Krugman

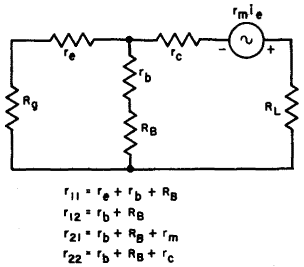
Fig. 6-5. Basic resistance controlled negative resistance circuit.

The preceding paragraphs indicate that transistor oscillators can be designed as equivalents for all the known types of vacuum-tube oscillators that use an external feedback path. In addition, the unique property of a transistor that furnishes current gain can also be used to design many other novel types of oscillators.

In the earlier chapters it was found that the point-contact transistor, by virtue of its ability to multiply the input current (r_m greater than r_c), is characterized by negative input and output resistances over part of its operating range. It is feasible, therefore, to use the point-contact transistor in this region to design oscillator circuits that do not require external feedback paths. As one engineer put it, "An oscillator is a poorly designed amplifier." This observation is particularly applicable in the case of the negative-resistance oscillator. The conditional stability equation for a point contact transistor was specified in Chapter 4 as: (r₁₁ + R_g) (R_L + r₂₂) - r₁₂r₂₁ must be greater than zero. Thus for the transistor to be unstable, that is for it to exhibit negative resistance characteristics, requires:

In general, external resistance can be added to any of the three electrode leads, as illustrated in Fig. 6-5. Substituting the transistor parameter values into equation 6-1 results in:

(r_e + r_b + R_B + R_g) (R_L + r_b + R_B + r_c) - (r_b + R_B)(r_b + R_B + r_m) < 0

Neglecting r_e and r_b as compared to R_B, r_c, and r_m, this becomes:

(R_B + R_g) (R_L + R_B + r_c) - R_B (R_B + r_m)< 0

and multiplying out

R_BR_L + R_B² + R_Br_c + Rg^RL + R_gR_B + R_gr_c - R_B² - R_Br_m < 0

which becomes:

R_g(R_L + r_c) + R_B(R_L + R_g) - R_B (r_m - r_c) < 0

Notice that when r_m is less than r_c (as in the case of the junction transistor) , the condition for oscillation cannot be satisfied. This re-emphasizes the fact that negative-resistance oscillators can only be designed using the point-contact transistor. Notice also in this equation that if both R_L and r_g are small compared to the value of (r_m - r_c), the conditional equation is primarily controlled by the value of R_B. The higher the value of R_B, the more definite the instability. Furthermore, as the external collector and emitter resistances are increased in value, a higher resistance of R_B is required to assure circuit oscillation. The control of oscillation in negative-resistance transistor oscillators, then, is determined by the following three factors, either separately or in combination: the external resistance of the emitter lead (a low value favors oscillation), the external resistance of the base lead (a high value favors oscillation), and the external resistance of the collector lead (a low value favors oscillation).