Negative Resistance and Transistor Stability

Author: Leonard Krugman

Consider the general expression for input resistance

It is evident that the input resistance can have a negative value. The input resistance r₁ is positive as long as r₁₁ is greater than. This condition is most difficult to attain when the output is shorted, namely when R_L = 0. For the transistor to be stable under this condition, r₁₁r₂₂ must be greater than r₁₂r₂₁. The stability factor is the ratio of r₁₂r₂₁ to r₁₁r₂₂. The stability factor 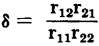must be less than unity for short-circuit stability. Substituting the equivalent transistor parameters for the grounded base connection into the stability equation, the following relationship is obtained:

Expanding equation 3-42,

r_cr_e + r_cr_b + r_br_e + r_b² > r_hr_m + r_b²

Dividing through by r_b

This equation emphasizes the importance of the backward transfer resistance r_b, since when r_b = 0, the transistor must have a positive input resistance.

On the other hand, if the value of r_b is increased by adding external resistance, it is possible to reach a condition where a normally positive input resistance becomes negative. Notice, however, that increasing the total base resistance eventually causes the input resistance to become negative only if r_e + r_c is less than r_m. In the case of the junction transistor, r_c is always greater than r_m, and increasing the base resistance cannot produce a negative input resistance.

The conditions for negative output resistance are obtained similarly. In the general output resistance equation,

the output resistance r_o is positive provided that r₂₂ is greater than

This condition for stability is most difficult to meet when the generator resistance is equal to zero. For the transistor to be stable under this condition, r_nr₂₂ again must be greater than r₁₂r₂₁. The same stability factor and equations then exist for both the input and output resistances. It is evident, then, that one method of fabricating a transistor oscillator is by adding sufficient resistance to the base arm. Typical circuits incorporating this principle will be considered in Chapter 6.