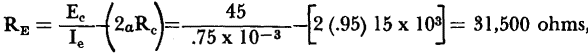| Transistor Basics is a free introductory textbook on transistors and their basic applications. See the editorial for more information.... |

|

Home  Transistor Oscillators Transistor Oscillators  Negative-Resistance Oscillators Negative-Resistance Oscillators  Bias Selection Bias Selection |
||||






|
||||
|
Bias SelectionAuthor: Leonard Krugman
Ee = REIe. The two conditional equations can be combined to evaluate RE in terms of known quantities:
Since RE also equals As a numerical example, if the values associated with Fig. 6-10 (B) are used so that the bias current at the center of the negative resistance region is Ie = 0.75 ma, then
and Ee = IeRE = .75 × 10-3 × 31.5 × 103 = 23.6 volts. The negative resistance of the oscillator is equal to the slope of the characteristics in that region. Then
This value defines the maximum limit of the impedance of the L-C series emitter circuit at resonance.
|
||||
Home  Transistor Oscillators Transistor Oscillators  Negative-Resistance Oscillators Negative-Resistance Oscillators  Bias Selection Bias Selection |
||||
Last Update: 2010-11-17



 , equation 6-2 limits the value of the emitter bias battery to less than that of Ec. The limiting value of Ee = Ec is reached when Rc = 0.
, equation 6-2 limits the value of the emitter bias battery to less than that of Ec. The limiting value of Ee = Ec is reached when Rc = 0.