Electron Lenses

Author: J.B. Hoag

Fig. 21 B. A double-gauze electron lens. (From E. & N. P.)

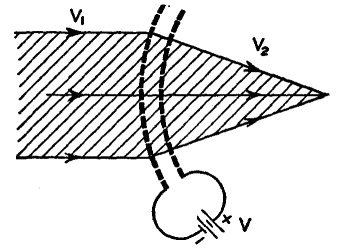
In Fig. 21 B, the heavy dashed lines represent two metal gauzes, curved as shown and electrically charged by the battery V, with positive on the right-hand gauze and negative on the left-hand gauze. An electric field is, therefore, established between the gauzes. Its direction is from the positive to the negative. This is the direction of the force action upon positive charges. A stream of electrons, whose velocity is represented by the symbol v₁,comes from the left and enters the electric field. Remember that electrons are negatively charged. When they enter the region between the two gauzes, the electric field tries to bend them immediately along its lines of force. Their forward momentum, however, opposes this deflection. As a result, they travel along a curved path which more and more approaches that of the electrostatic lines of force. After passing through both gauzes, they continue along their new paths at the higher velocity v₂. The shaded area in the figure indicates the total region occupied by the electrons. The fact that the various electrons in this region come to a common focal point is only possible if the gauzes have been so curved that the resultant of the electrostatic deflecting force and the forward momentum of the electrons is directly proportional to the distance of the electrons from the axis.

The first electron lens to be treated mathematically is shown in Fig. 21 C.

Fig. 21 C. A single-aperture electron lens. (From E. & N. P.)

	There's an interactive simulation available on the "Learning by Simulations" Web site which allows to calculate the trajectories of charged particles in an electrostatic field.

This is called a diaphragm-hole or single-aperture lens. A parallel beam of electrons in the metal can (indicated by the heavy lines at the left of the figure) are deflected by the distorted electrostatic field in the hole at the end of the can, in such a manner as to be converged toward the metal plate (represented by the heavy vertical line at the right of the figure). By proper adjustment of the voltage of the battery V and the speed of the electrons, they can be brought to a sharp focal point on the metal plate.

Fig. 21 D. A two-aperture lens

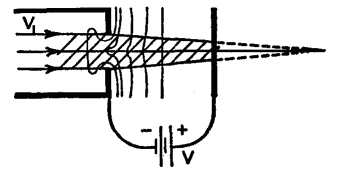
Combinations of two or more diaphragm lenses, as in Fig. 21 D, have been used to produce magnified, inverted, real images of the surface of filaments, thus permitting detailed studies of the emission of electrons from various minute portions of cathodes or hot filaments.

An electron lens can be formed by means of two metal cylinders charged to different potentials. These are known as double-cylinder lenses. When a parallel bundle of electrons, traveling at a constant velocity, as in Fig. 21 E, enters the electrostatic field between the ends of the cylinders, it is converged toward a point, 0 in the figure, because the electrons must assume a compromise motion between their forward paths and the direction of the electrostatic lines of force.

Fig. 21 E. A double-cylinder lens. (From E. & N. P.)

After passing the gap between the two cylinders, the electrons find themselves in an electrostatic field which causes them to diverge. But, at this point, the electrons are traveling faster, having been accelerated across the gap by the voltage V. Their momentum being greater and the electric field being the same, their divergence will not be as great as their convergence. Hence they continue down the cylinder, converging toward a more distant point.

Fig. 21 F. A short-focus double-cylinder lens. (From E. & N. P.)

In Fig. 21 F, the second cylinder is larger than the first cylinder, with the result that the electrostatic lines spread out more in the second cylinder. This means that the electrostatic field in this region is weaker and its divergent action on the electrons is less. Hence the electrons come to a focus sooner than in the case where the two cylinders are of the same diameter.