| The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry. |

|

Home  Analytic Geometry Analytic Geometry  Triangle Triangle  Altitudes of a Triangle Altitudes of a Triangle |
|||||||||
| See also: Construction of a Triangle, Properties of a Right Triangle, Circumcircle of a Triangle, Excircle of a Triangle | |||||||||






|
|||||||||
Altitudes of a Triangle
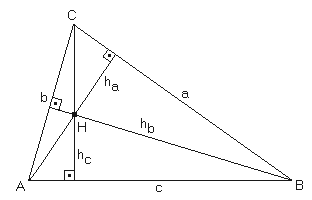 The heights (or altitudes) ha, hb, and hc of a triangle are the perpendiculars through the corner points to the opposite sides. All three altitudes intersect at the orthocenter H. The position of H depends on the form of of the triangle:
The heights (or altitudes) ha, hb, and hc of a triangle are the perpendiculars through the corner points to the opposite sides. All three altitudes intersect at the orthocenter H. The position of H depends on the form of of the triangle:
The following equations are valid for the relations between the altitudes, the angles and sides:
ha = b There are a two theorems concerning the altitudes of a triangle which can be used to construct triangles:
|
|||||||||
Home  Analytic Geometry Analytic Geometry  Triangle Triangle  Altitudes of a Triangle Altitudes of a Triangle |
|||||||||
Last Update: 2011-01-11


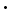 sin γ = c
sin γ = c