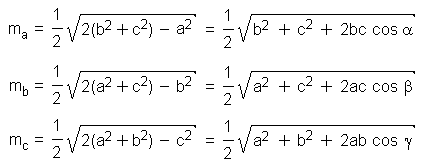The Compendium Geometry is an eBook providing facts, formulas and explanations about geometry.

Home Analytic Geometry Triangle Median and Centroid
See also: Construction of a Triangle, Properties of a Right Triangle 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Median and Centroid of a Triangle

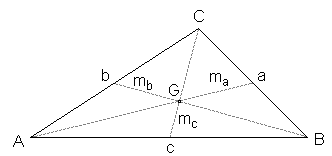A median of a triangle is a straight line through a vertex and the midpoint of the opposite side. The three medians ma, mb, and mc, intersect in a single point, the triangle's centroid.

For triangles made of homogeneous material (and with constant thickness) the centroid is also the triangle's center of gravity G. The centroid cuts every median in the ratio 2:1, i.e. the distance between a vertex and the centroid is twice as long as the distance between the centroid and the midpoint of the opposite side.

The lengths of the medians are defined by the following equations:

Please note that any median cuts the triangle into two triangles which have two sides of equal length.

Home Analytic Geometry Triangle Median and Centroid

Last Update: 2010-12-06