| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Physical Chemistry Physical Chemistry  Acid-Base Equilibrium Acid-Base Equilibrium  Percent Ionization in Weak Acids Percent Ionization in Weak Acids |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Percent Ionization in Weak AcidsAuthor: John Hutchinson
Table 1 shows that the pH of 0.1M acid solutions varies from one weak acid to another. If we dissolve 0.1 moles of acid in a 1.0L solution, the fraction of those acid molecules which will ionize varies from weak acid to weak acid. For a few weak acids, using the data in table 1 we calculate the percentage of ionized acid molecules in 0.1M acid solutions in table 2.
We might be tempted to conclude from table 2 that we can characterize the strength of each acid by the percent ionization of acid molecules in solution. However, before doing so, we observe the pH of a single acid, nitrous acid, in solution as a function of the concentration of the acid.
In this case, "concentration of the acid" refers to the number of moles of acid that we dissolved per liter of water. Our observations are listed in table 3, which gives [H3O+], pH, and percent ionization as a function of nitrous acid concentration.
Since we know that gas phase reactions come to equilibrium under conditions determined by the equilibrium constant, we might speculate that the same is true of reactions in aqueous solution, including acid ionization. We therefore define an analogy to the gas phase reaction equilibrium constant. In this case, we would not be interested in the pressures of the components, since the reactants and products are all in solution. Instead, we try a function composed of the equilibrium concentrations:
The concentrations at equilibrium can be calculated from the data in table 3 for nitrous acid. [H3O+] is listed and [NO2-]=[H3O+]. Furthermore, if c0 is the initial concentration of the acid defined by the number of moles of acid dissolved in solution per liter of solution, then [HA]=c0-[H3O+]. Note that the contribution of [H2O(l)] to the value of the function K is simply a constant. This is because the "concentration" of water in the solution is simply the molar density of water, n(H2O)/V = 55.5M, which is not affected by the presence or absence of solute. All of the relevant concentrations, along with the function in equation 3 are calculated and tabulated in table 4.
We note that the function K in equation 3 is approximately, though only approximately, the same for all conditions analyzed in table 3. Variation of the concentration by a factor of 1000 produces a change in K of only 10% to 15%. Hence, we can regard the function K as a constant which approximately describes the acid ionization equilibrium for nitrous acid. By convention, chemists omit the constant concentration of water from the equilibrium expression, resulting in the acid ionization equilibrium constant, Ka, defined as:
From an average of the data in table 4, we can calculate that, at 25°C for nitrous acid, Ka=5
We make two final notes about the results in table 5. First, it is clear the larger the value of Ka, the stronger the acid. That is, when Ka is a larger number, the percent ionization of the acid is larger, and vice versa. Second, the values of Ka very over many orders of magnitude. As such, it is often convenient to define the quanity pKa, analogous to pH, for purposes of comparing acid strengths:
The value of pKa for each acid is also listed in table 5. Note that a small value of pKa implies a large value of Ka and thus a stronger acid. Weaker acids have larger values of pKa. Ka and pKa thus give a simple quantitative comparison of the strength of weak acids.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Home  Physical Chemistry Physical Chemistry  Acid-Base Equilibrium Acid-Base Equilibrium  Percent Ionization in Weak Acids Percent Ionization in Weak Acids |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Last Update: 2011-04-07


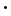 10-3
10-3 H3O+(aq) + NO2-(aq)
H3O+(aq) + NO2-(aq)
