| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Bonding Bonding  Chemical Bonding and Molecular Energy Levels Chemical Bonding and Molecular Energy Levels  Bonding with a Single Electron Bonding with a Single Electron |
|||||






|
|||||
Bonding with a Single ElectronAuthor: Hans Lohninger
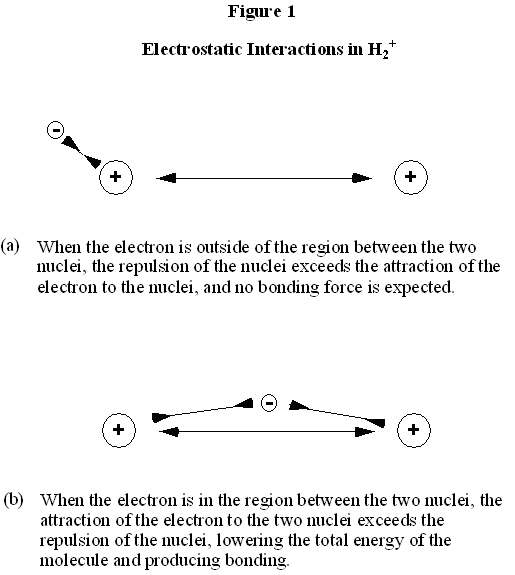
We began our analysis of the energies and motions of the electrons in atoms by observing the properties of the simplest atom, hydrogen, with a single electron. Similarly, to understand the energies and motions of electrons which lead to chemical bonding, we begin our observations with the simplest particle with a chemical bond, which is the H2+ molecular ion. Each hydrogen nucleus has a charge of +1. An H2+ molecular ion therefore has a single electron. It seems inconsistent with our notions of valence that a single electron, rather than an electron pair, can generate a chemical bond. However, these concepts have been based on observations on molecules, not molecular ions like H2+. And it is indeed found that H2+ is a stable bound molecular ion. What forces and motions hold the two hydrogen nuclei close together in the H2+ ion? It is worth keeping in mind that the two nuclei must repel one another, since they are both positively charged. In the absence of the electron, the two nuclei would accelerate away from one another, rather than remaining in close proximity. What is the role of the electron? Clearly, the electron is attracted to both nuclei at the same time, and, in turn, each nucleus is attracted to the electron. The effect of this is illustrated in Fig. 1. In Fig. 1a, the electron is “outside” of the two nuclei. In this position, the electron is primarily attracted to the nucleus on the left, to which it is closer. More importantly, the nucleus on the right feels a greater repulsion from the other nucleus than attraction to the electron, which is farther away. As a result, the nucleus on the right experiences a strong force driving it away from the hydrogen atom on the left. This arrangement does not generate chemical bonding, therefore. By contrast, in Fig. 1b, the electron is between the two nuclei. In this position, the electron is roughly equally attracted to the two nuclei, and very importantly, each nucleus feels an attractive force to the electron which is greater than the repulsive force generated by the other nucleus. Focusing on the electron’s energy, the proximity of the two nuclei provides it a doubly attractive environment with a very low potential energy. If we tried to pull one of the nuclei away, this would raise the potential energy of the electron, since it would lose attraction to that nucleus. Hence, to pull one nucleus away requires us to add energy to the molecular ion. This is what is meant by a chemical bond: the energy of the electrons is lower when the atoms are in close proximity than when the atoms are far part. This “holds” the nuclei close together, since we must do work (add energy) to take the nuclei apart.
Note that the chemical bond in Fig. 1b results from the electron’s position between the nuclei. On first thought, this appears to answer our question of what we mean by “sharing an electron pair” to form a chemical bond. An electron positioned between two nuclei is “shared” to the extent that its potential energy is lowered due to attraction to both nuclei simultaneously. On second thought, though, this description must be inaccurate. We have learned our study of Energy Levels in Atoms that an electron must obey the uncertainty principle and that, as a consequence, the electron does not have a definite position, between the nuclei or otherwise. We can only hope to specify a probability for observing an electron in a particular location. This probability is, from quantum mechanics, provided by the wave function. What does this probability distribution look like for the H2+ molecular ion? To answer this question, we begin by experimenting with a distribution that we know: the 1s electron orbital in a hydrogen atom. This we recall has the symmetry of a sphere, with equal probability in all directions away from the nucleus. To create an H2+ molecular ion from a hydrogen atom, we must add a bare second hydrogen nucleus (an H+ion). Imagine bringing this nucleus closer to the hydrogen atom from a very great distance (see Fig. 2a). As the H+ion approaches the neutral atom, both the hydrogen atom’s nucleus and electron respond to the electric potential generated by the positive charge. The electron is attracted and the hydrogen atom nucleus is repelled. As a result, the distribution of probability for the electron about the nucleus must become distorted, so that the electron has a greater probability of being near the H+ ion and the nucleus has a greater probability of being farther from the ion. This distortion, illustrated in Fig. 2b, is called “polarization”: the hydrogen atom has become like a “dipole”, with greater negative charge to one side and greater positive charge to the other.
This polarization must increase as the H+ ion approaches the hydrogen atom until, eventually, the electron orbital must be sufficiently distorted that there is equal probability for observing the electron in proximity to either hydrogen nucleus (see Fig. 2c). The electron probability distribution in Fig. 2c now describes the motion of the electron, not in a hydrogen atom, but in an H2+ molecular ion. As such, we refer to this distribution as a “molecular orbital.” We note that the molecular orbital in Fig. 2c is more delocalized than the atomic orbital in Fig. 2a, and this is also important in producing the chemical bond. We recall from the discussion of Atomic Energy Levels that the energy of an electron in an orbital is determined, in part, by the compactness of the orbital. The more the orbital confines the motion of the electron, the higher is the kinetic energy of the electron, an effect we referred to as the “confinement energy.” Applying this concept to the orbitals in Fig. 2, we can conclude that the confinement energy is lowered when the electron is delocalized over two nuclei in a molecular orbital. This effect contributes significantly to the lowering of the energy of an electron resulting from sharing by two nuclei. Recall that the electron orbitals in the hydrogen atom are described by a set of quantum numbers. One of these quantum numbers is related to the symmetry or shape of the atomic orbital and is generally depicted by a letter. Recall that an “s” orbital is spherical in shape, and a “p” orbital has two lobes aligned along one axis. Similarly, the molecular orbitals for the H2+ molecular ion are described by a set of numbers which give the symmetry (or shape) of the orbital. For our purposes, we need only one of these descriptors, based on the symmetry of the orbital along the bond: if the molecular orbital has the symmetry of a cylinder, we refer to it as a "σ orbital". The orbital in Fig. 2c satisfies this condition. We conclude that chemical bonding results from an electron in a molecular orbital which has substantial probability for the electron to be between two nuclei. However, this example illustrates chemical bonding with a single electron. Our rules of valence indicate that bonding typically occurs with a pair of electrons, rather than a single electron. Furthermore, this model of bonding does not tell us how to handle molecules with many electrons (say, F2) where most of the electrons do not participate in the bonding at all.
|
|||||
Home  Bonding Bonding  Chemical Bonding and Molecular Energy Levels Chemical Bonding and Molecular Energy Levels  Bonding with a Single Electron Bonding with a Single Electron |
|||||
Last Update: 2011-02-16