| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Molecules Molecules  The Kinetic Molecular Theory The Kinetic Molecular Theory  Boyle's Law Boyle's Law |
|||||||||






|
|||||||||
Boyle's LawAuthor: John Hutchinson
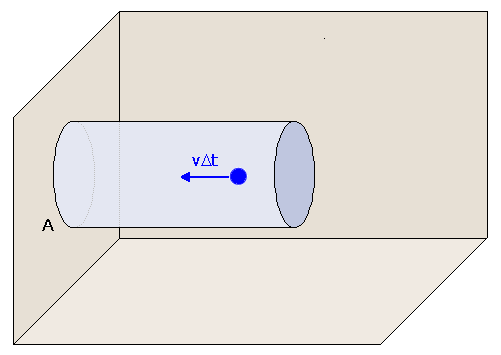
To calculate the pressure generated by a gas of N particles contained in a volume V, we must calculate the force F generated per area A by collisions against the walls. To do so, we begin by determining the number of collisions of particles with the walls. The number of collisions we observe depends on how long we wait. Let's measure the pressure for a period of time Δt and calculate how many collisions occur in that time period. For a particle to collide with the wall within the time Δt, it must start close enough to the wall to impact it in that period of time. If the particle is travelling with speed v, then the particle must be within a distance vΔt of the wall to hit it. Also, if we are measuring the force exerted on the area A, the particle must hit that area to contribute to our pressure measurement. For simplicity, we can view the situation pictorially here. We assume that the particles are moving perpendicularly to the walls. (This is clearly not true. However, very importantly, this assumption is only made to simplify the mathematics of our derivation. It is not necessary to make this assumption, and the result is not affected by the assumption). In order for a particle to hit the area A marked on the wall, it must lie within the cylinder shown, which is of length vΔt and cross-sectional area A. The volume of this cylinder is AvΔt, so the number of particles contained in the cylinder is AvΔtN/V.
Not all of these particles collide with the wall during Δt, though, since most of them are not traveling in the correct direction. There are six directions for a particle to go, corresponding to plus or minus direction in x, y, or z. Therefore, on average, the fraction of particles moving in the correct direction should be 1/6, assuming as we have that the motions are all random. Therefore, the number of particles which impact the wall in time Δt is AvΔtN/6V. The force generated by these collisions is calculated from Newton’s equation, F=ma, where a is the acceleration due to the collisions. Consider first a single particle moving directly perpendicular to a wall with velocity v as in figure 3. We note that, when the particle collides with the wall, the wall does not move, so the collision must generally conserve the energy of the particle. Then the particle’s velocity after the collision must be -v, since it is now travelling in the opposite direction. Thus, the change in velocity of the particle in this one collision is 2v. Multiplying by the number of collisions in Δt and dividing by the time Δt, we find that the total acceleration (change in velocity per time) is 2ANv2/6V, and the force imparted on the wall due collisions is found by multiplying by the mass of the particles:
To calculate the pressure, we divide by the area A, to find that
or, rearranged for comparison to Boyle's Law,
Since we have assumed that the particles travel with constant speed v, then the right side of this equation is a constant. Therefore the product of pressure times volume, PV, is a constant, in agreement with Boyle's Law. Furthermore, the product PV is proportional to the number of particles, also in agreement with the Law of Combining Volumes. Therefore, the model we have developed to describe an ideal gas is consistent with our experimental observations. We can draw two very important conclusions from this derivation. First, the inverse relationship observed between pressure and volume and the independence of this relationship on the type of gas analyzed are both due to the lack of interactions between gas particles. Second, the lack of interactions is in turn due to the great distances between gas particles, a fact which will be true provided that the density of the gas is low.
|
|||||||||
Home  Molecules Molecules  The Kinetic Molecular Theory The Kinetic Molecular Theory  Boyle's Law Boyle's Law |
|||||||||
Last Update: 2011-02-16