| General Chemistry is a free introductory textbook on chemistry. See the editorial for more information.... |

|

Home  Molecules Molecules  The Kinetic Molecular Theory The Kinetic Molecular Theory  Interpretation of Temperature Interpretation of Temperature |
|||||||






|
|||||||
Interpretation of TemperatureAuthor: John Hutchinson
The absence of temperature in the above derivation is notable. The other gas properties have all been incorporated, yet we have derived an equation which omits temperature all together. The problem is that, as we discussed at length above, the temperature was somewhat arbitrarily defined. In fact, it is not precisely clear what has been measured by the temperature. We defined the temperature of a gas in terms of the volume of mercury in a glass tube in contact with the gas. It is perhaps then no wonder that such a quantity does not show up in a mechanical derivation of the gas properties. On the other hand, the temperature does appear prominently in the Ideal Gas Law. Therefore, there must be a greater significance (and less arbitrariness) to the temperature than might have been expected. To discern this significance, we rewrite the last equation above in the form:
The last quantity in parenthesis can be recognized as the kinetic energy of an individual gas particle, and N(mv2/2) must be the total kinetic energy (KE) of the gas. Therefore
Now we insert the Ideal Gas Law for PV to find that
This is an extremely important conclusion, for it reveals the answer to the question of what property is measured by the temperature. We see now that the temperature is a measure of the total kinetic energy of the gas. Thus, when we heat a gas, elevating its temperature, we are increasing the average kinetic energy of the gas particles, causing then to move, on average, more rapidly.
|
|||||||
Home  Molecules Molecules  The Kinetic Molecular Theory The Kinetic Molecular Theory  Interpretation of Temperature Interpretation of Temperature |
|||||||
Last Update: 2011-02-16


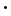 1/2mv2
1/2mv2