Oxidized Buckminsterfullerene

Author: John Hutchinson

We begin by considering a fairly simple reaction on a rather elegant molecule. One oxidized form of buckminsterfullerene C₆₀ is C₆₀O₃, with a three oxygen bridge as shown in figure 1.

Figure 1: Oxidized Buckminsterfullerene.

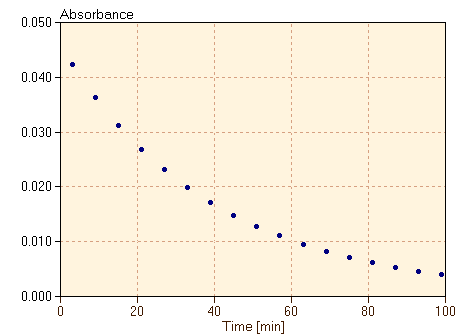
C₆₀O₃ is prepared from C₆₀ dissolved in toluene solution at temperatures of 0°C or below. When the solution is warmed, C₆₀O₃ decomposes, releasing O₂ and creating C₆₀O in a reaction which goes essentially to completion. We can actually watch this process happen in time by measuring the amount of light of a specific frequency absorbed by the C₆₀O₃ molecules, called the absorbance. The absorbance is proportional to the concentration of the C₆₀O₃ in the toluene solution, so observing the absorbance as a function of time is essentially the same as observing the concentration as a function of time. One such set of data is given in table 1, and is shown in the graph in figure 2.

Table 1: Oxidized Buckminsterfullerene Absorbance during Thermal Decomposition at 23°C

Time [min]	C60O3 Absorbance
3	0.04241
9	0.03634
15	0.03121
21	0.02680
27	0.02311
33	0.01992
39	0.01721
45	0.01484
51	0.01286
57	0.01106
63	0.00955
69	0.00827
75	0.00710
81	0.00616
87	0.00534
93	0.00461
99	0.00395

Figure 2: Oxidized Buckminsterfullerene Absorbance.

The rate at which the decomposition reaction is occurring is clearly related to the rate of change of the concentration [C₆₀O₃], which is proportional to the slope of the graph in figure 2. Therefore, we define the rate of this reaction as

Rate = -d[C60O3]/dt ~ -Δ[C60O3]/Δt

[1]

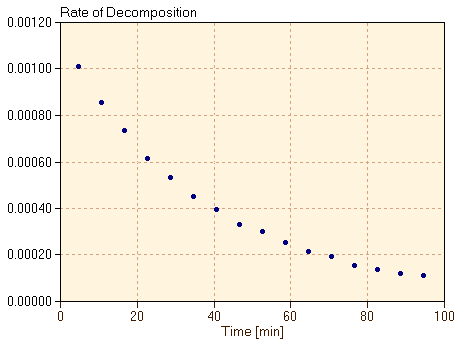
We want the rate of reaction to be positive, since the reaction is proceeding forward. However, because we are measuring the rate of disappearance of the reactant in this case, that rate is negative. We include a negative sign in this definition of rate so that the rate in equation 1 is a positive number. Note also that the slope of the graph in figure 2 should be taken as the derivative of the graph, since the graph is not a straight line. We will approximate that derivative by estimating the slope at each time in the data, taking the change in the absorbance of the C₆₀O₃ divided by the change in time at each time step. The rate, calculated in this way, is plotted as a function of time in figure 3.

Figure 3: Rate of Decomposition.

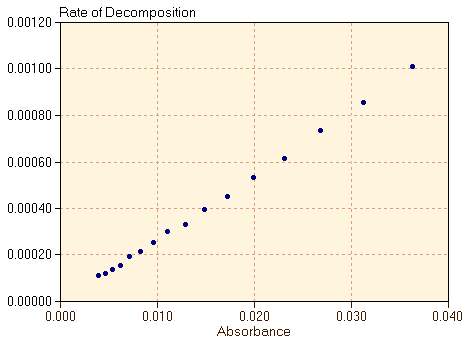
It is clear that the slope of the graph in figure 2 changes over the course of time. Correspondingly, figure 3 shows that the rate of the reaction decreases as the reaction proceeds. The reaction is at first very fast but then slows considerably as the reactant C₆₀O₃ is depleted.

The shape of the graph for rate versus time (figure 3) is very similar to the shape of the graph for concentration versus time (figure 2). This suggests that the rate of the reaction is related to the concentration of C₆₀O₃ at each time. Therefore, in figure 4, we plot the rate of the reaction, defined in equation 1 and shown in figure 3, versus the absorbance of the C₆₀O₃.

Figure 4: Rate versus Concentration.

We find that there is a very simple proportional relationship between the rate of the reaction and the concentration of the reactant. Therefore, we can write

Rate = - d[C60O3]/dt = k[C60O3]

[2]

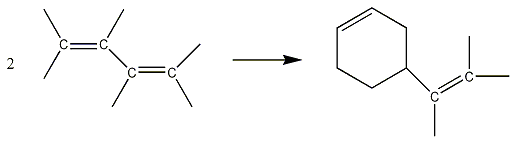
where k is a proportionality constant. This equation shows that, early in the reaction when [C₆₀O₃] is large, the reaction proceeds rapidly, and that as C₆₀O₃ is consumed, the reaction slows down. equation 2 is an example of a rate law, expressing the relationship between the rate of a reaction and the concentrations of the reactant or reactants. Rate laws are expressions of the relationship between experimentally observed rates and concentrations.

As a second example of a reaction rate, we consider the dimerization reaction of butadiene gas, CH₂=CH-CH=CH₂. Two butadiene molecules can combine to form vinylcyclohexene, shown in figure 5.

Figure 5: Dimerization of Butadiene to Vinylcyclohexene.

The following table provides experimental data on the gas phase concentration of butadiene [C₄H₆] as a function of time at T=250°C.

Table 2: Dimerization of Butadiene at 250°C

Time (s)	[C4H6] (M)	Rate (M/s)	Rate [C4H6]	Rate [C4H6]2
0	0.0917	9.48×10-6	1.03×10-4	1.13×10-3
500	0.0870	8.55×10-6	9.84×10-5	1.13×10-3
1000	0.0827	7.75×10-6	9.37×10-5	1.13×10-3
1500	0.0788	7.05×10-6	8.95×10-5	1.14×10-3
2000	0.0753	6.45×10-6	8.57×10-5	1.14×10-3
2500	0.0720	5.92×10-6	8.22×10-5	1.14×10-3
3000	0.0691	5.45×10-6	7.90×10-5	1.14×10-3
3500	0.0664	5.04×10-6	7.60×10-5	1.14×10-3
4000	0.0638	4.67×10-6	7.32×10-5	1.15×10-3

We can estimate the rate of reaction at each time step as in equation 1, and these data are presented in table 2 as well. Again we see that the rate of reaction decreases as the concentration of butadiene decreases. This suggests that the rate is given by an expression like equation 2. To test this, we calculate Rate/[C₄H₆] in table 2 for each time step. We note that this is not a constant, so equation 2 does not describe the relationship between the rate of reaction and the concentration of butadiene. Instead we calculate Rate/[C₄H₆]² in table 2. We discover that this ratio is a constant throughout the reaction. Therefore, the relationship between the rate of the reaction and the concentration of the reactant in this case is given by

Rate = -d[C4H6]/dt = k[C4H6]2

[3]

which is the rate law for the reaction in figure 5. This is a very interesting result when compared to equation 2. In both cases, the results demonstrate that the rate of reaction depends on the concentration of the reactant. However, we now also know that the way in which the rate varies with the concentration depends on what the reaction is. Each reaction has its own rate law, observed experimentally.