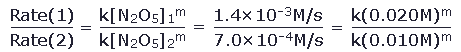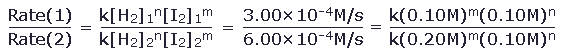Rate Laws and the Order of Reaction

Author: John Hutchinson

We would like to understand what determines the specific dependence of the reaction rate on concentration in each reaction. In the first case considered above, the rate depends on the concentration of the reactant to the first power. We refer to this as a first order reaction. In the second case above, the rate depends on the concentration of the reactant to the second power, so this is called a second order reaction. There are also third order reactions, and even zero^th order reactions whose rates do not depend on the amount of the reactant. We need more observations of rate laws for different reactions.

The approach used in the previous section to determine a reaction's rate law is fairly clumsy and at this point difficult to apply. We consider here a more systematic approach. First, consider the decomposition of N₂O₅(g).

2N₂O₅(g) 4NO₂(g) + O₂(g)

Rate = k[N2O5]m

[4]

so we need to determine the exponent m. For example, at 25°C we observe that the rate of decomposition is 1.4×10^-3M/s when the concentration of N₂O₅ is 0.020M. If instead we begin we [N₂O₅]=0.010M, we observe that the rate of decomposition is 7.0×10^-4M/s. We can compare the rate from the first measurement Rate(1) to the rate from the second measurement Rate(2). From equation 4, we can write that

[5]

This can be simplified on both sides of the equation to give 2.0 = 2.0^m Clearly, then m=1, and the decomposition is a first order reaction. We can also then find the first order rate constant k for this reaction by simply plugging in one of the initial rate measurements to equation 4. We find that k = 0.070 s^-1.

This approach to finding reaction order is called the method of initial rates, since it relies on fixing the concentration at specific initial values and measuring the initial rate associated with each concentration.

So far we have considered only reactions which have a single reactant. Consider a second example of the method of initial rates involving the reaction of hydrogen gas and iodine gas:

H2(g) + I2(g) 2HI(g)

[6]

In this case, we expect to find that the rate of the reaction depends on the concentrations for both reactants. As such, we need more initial rate observations to determine the rate law. In table 3, observations are reported for the initial rate for three sets of initial concentrations of H₂ and I₂.

Table 3: Hydrogen Gas and Iodine Gas Initial Rate Data at 700K

Experiment	[H2]0 (M)	[I2]0 (M)	Rate (M/sec)
1	0.10	0.10	3.00×10-4
2	0.20	0.10	6.00×10-4
3	0.20	0.20	1.19×10-3

Following the same process we used in the N₂O₅ example, we write the general rate law for the reaction as

Rate = k[H2]n[I2]m

[7]

By comparing experiment 1 to experiment 2, we can write

[8]

This simplifies to

0.50 = 0.50^m1.00ⁿ

Rate = k[H2][I2]

[9]

Once we know the rate law, we can use any of the data from table 3 to determine the rate constant, simply by plugging in concentrations and rate into equation 9. We find that k = 3.00×10^-2 (Ms)^-1.

This procedure can be applied to any number of reactions. The challenge is preparing the initial conditions and measuring the initial change in concentration precisely versus time. Table 4 provides an overview of the rate laws for several reactions. A variety of reaction orders are observed, and they cannot be easily correlated with the stoichiometry of the reaction.

Table 4: Rate Laws for Various Reactions

Reaction Rate	Law
2 NO(g) + O2(g) 2 NO2(g)	Rate=k[NO]2[O2]
2 NO(g) + 2 H2(g) 2 N2(g) + 2 H2O(g)	Rate=k[NO]2[H2]
2 ICl(g) + H2(g) 2 HCl(g) + I2(g)	Rate=k[ICl][H2]
2 N2O5(g) 4 NO2(g) + O2(g)	Rate=k[N2O5]
2 NO2(g) + F2(g) 2 NO2F(g)	Rate=k[NO2][F2]
2 H2O2(aq) 2 H2O(l) + O2(g)	Rate=k[H2O2]
H2(g) + Br2(g) 2 HBr(g)	Rate=k[H2][Br2]0.5
O3(g) + Cl(g) O2(g) + ClO(g)	Rate=k[O3][Cl]